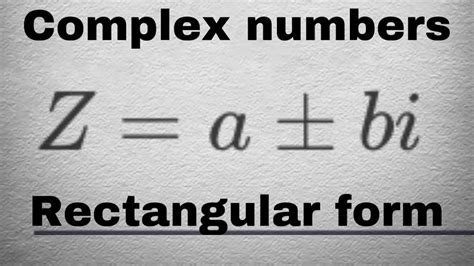5 Ways To Write Complex Numbers In Rectangular Form

Quick Links :

Complex numbers have been a cornerstone of mathematics and science for centuries, allowing us to extend the real number system to include numbers that can be expressed in the form a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit, satisfying the equation i^2 = -1. One of the fundamental aspects of complex numbers is their representation in rectangular form, which is crucial for understanding and manipulating complex numbers in various mathematical and scientific applications.

Understanding Rectangular Form

The rectangular form of a complex number, also known as the Cartesian form, is a way of expressing complex numbers in terms of their real and imaginary components. It is a powerful tool for performing arithmetic operations on complex numbers and for visualizing their geometric representation on the complex plane. In this article, we will explore five different ways to write complex numbers in rectangular form, highlighting their benefits and applications.

Method 1: Using the Standard Form

The most straightforward way to write a complex number in rectangular form is by using the standard form, which is given by:

z = a + bi

where 'a' is the real part and 'b' is the imaginary part of the complex number. For example, the complex number 3 + 4i can be written in rectangular form as z = 3 + 4i.

Benefits of Rectangular Form

The rectangular form of complex numbers has several benefits, including:

• Simplifying arithmetic operations: The rectangular form makes it easier to perform arithmetic operations such as addition, subtraction, multiplication, and division on complex numbers.
• Visualizing complex numbers: The rectangular form allows us to visualize complex numbers on the complex plane, which is a powerful tool for understanding their geometric properties.
• Solving equations: The rectangular form is essential for solving equations involving complex numbers, such as quadratic equations and polynomial equations.

Method 2: Using the Polar Form

Another way to write complex numbers in rectangular form is by using the polar form, which is given by:

z = r(cosθ + isinθ)

where 'r' is the magnitude (or modulus) of the complex number and 'θ' is its argument (or angle). For example, the complex number 3 + 4i can be written in polar form as z = 5(cosθ + isinθ), where r = 5 and θ = arctan(4/3).

Converting between Rectangular and Polar Forms

Converting between rectangular and polar forms is a crucial aspect of working with complex numbers. The following formulas can be used to convert between the two forms:

• Rectangular to polar: r = √(a^2 + b^2), θ = arctan(b/a)
• Polar to rectangular: a = rcosθ, b = rsinθ

Method 3: Using the Exponential Form

The exponential form is another way to write complex numbers in rectangular form, which is given by:

z = re^(iθ)

where 'r' is the magnitude (or modulus) of the complex number and 'θ' is its argument (or angle). For example, the complex number 3 + 4i can be written in exponential form as z = 5e^(iθ), where r = 5 and θ = arctan(4/3).

Applications of Complex Numbers

Complex numbers have numerous applications in mathematics, science, and engineering, including:

• Signal processing: Complex numbers are used to represent and analyze signals in various fields such as electrical engineering, telecommunications, and medical imaging.
• Control theory: Complex numbers are used to model and control systems in fields such as aerospace engineering, mechanical engineering, and chemical engineering.
• Quantum mechanics: Complex numbers are used to describe the behavior of particles at the atomic and subatomic level.

Method 4: Using the Trigonometric Form

The trigonometric form is another way to write complex numbers in rectangular form, which is given by:

z = a + bi = r(cosθ + isinθ)

where 'a' and 'b' are the real and imaginary parts of the complex number, 'r' is its magnitude (or modulus), and 'θ' is its argument (or angle). For example, the complex number 3 + 4i can be written in trigonometric form as z = 5(cosθ + isinθ), where r = 5 and θ = arctan(4/3).

Geometric Representation of Complex Numbers

The geometric representation of complex numbers is a powerful tool for understanding their properties and behavior. The complex plane is a two-dimensional plane where the real part of the complex number is plotted on the x-axis and the imaginary part is plotted on the y-axis.

Method 5: Using the Algebraic Form

The algebraic form is another way to write complex numbers in rectangular form, which is given by:

z = a + bi = (a + √(-1)b)

where 'a' and 'b' are the real and imaginary parts of the complex number. For example, the complex number 3 + 4i can be written in algebraic form as z = 3 + √(-1)4.

Conclusion and Next Steps

In conclusion, there are several ways to write complex numbers in rectangular form, each with its own benefits and applications. Understanding the different forms of complex numbers is essential for working with them in various mathematical and scientific contexts. We hope that this article has provided a comprehensive introduction to the rectangular form of complex numbers and has inspired you to explore further.

What do you think about the rectangular form of complex numbers? Share your thoughts and questions in the comments below!