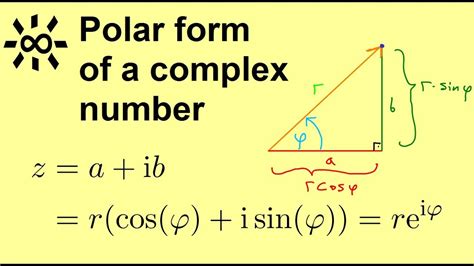Convert Complex Numbers To Polar Form In 3 Easy Steps

Quick Links :

Complex numbers have been a cornerstone of mathematics and engineering for centuries, allowing us to extend the real number system to solve problems that cannot be tackled within the confines of real numbers alone. One of the most powerful representations of complex numbers is the polar form, which offers a clear geometric interpretation and simplifies many operations. In this article, we will delve into the importance of converting complex numbers to polar form and provide a step-by-step guide on how to do it with ease.

Why Convert to Polar Form?

Converting complex numbers to polar form is essential for various applications in mathematics, physics, and engineering. The polar form of a complex number offers several advantages:

• Geometric Interpretation: It provides a clear and intuitive geometric representation, making it easier to visualize and understand complex number operations.
• Simplifies Operations: Many operations, such as multiplication and division, become significantly simpler in polar form, making calculations more efficient.
• Applications in Engineering and Physics: Polar form is crucial for representing and analyzing signals in electronics and telecommunications, as well as for solving problems in mechanics and electromagnetism.

Understanding Polar Form Basics

Before we dive into the conversion steps, let's quickly review the basics of polar form. A complex number (z = a + bi) can be represented in polar form as (z = r(\cos(\theta) + i\sin(\theta))), where:

• (r) is the modulus (or magnitude) of the complex number, representing the distance from the origin to the point in the complex plane.
• (\theta) is the argument (or angle) of the complex number, measured counterclockwise from the positive real axis.

Step 1: Calculate the Modulus (r)

The modulus (r) of a complex number (z = a + bi) is calculated using the formula:

[r = \sqrt{a^2 + b^2}]

This formula is derived from the Pythagorean theorem, considering the real part (a) and the imaginary part (b) as the legs of a right triangle, with (r) being the hypotenuse.

Example Calculation for Modulus

Given the complex number (z = 3 + 4i), we calculate the modulus as follows:

[r = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5]

Step 2: Calculate the Argument (\(\theta\))

The argument (\theta) can be found using the formula:

[\theta = \arctan\left(\frac{b}{a}\right)]

However, it's crucial to consider the quadrant in which the complex number lies, as the arctan function only returns values in the range (-\frac{\pi}{2}) to (\frac{\pi}{2}).

Example Calculation for Argument

Using the same complex number (z = 3 + 4i), we calculate the argument:

[\theta = \arctan\left(\frac{4}{3}\right)]

Considering the complex number is in the first quadrant (both (a) and (b) are positive), the calculated angle is correct. However, if the complex number were in a different quadrant, we would need to adjust (\theta) accordingly.

Step 3: Express the Complex Number in Polar Form

Once we have calculated (r) and (\theta), we can express the complex number in polar form as:

[z = r(\cos(\theta) + i\sin(\theta))]

Using the values from our example ((r = 5) and (\theta = \arctan\left(\frac{4}{3}\right))), the polar form of (z = 3 + 4i) is:

[z = 5\left(\cos\left(\arctan\left(\frac{4}{3}\right)\right) + i\sin\left(\arctan\left(\frac{4}{3}\right)\right)\right)]

This concludes our 3-step process for converting a complex number to polar form.

Conclusion and Next Steps

Converting complex numbers to polar form is a fundamental skill that opens up a wide range of possibilities for solving problems in mathematics, physics, and engineering. By following these three easy steps, you can ensure that your complex number representations are both accurate and efficient. Whether you're tackling advanced calculus, analyzing electrical circuits, or exploring the intricacies of quantum mechanics, the polar form of complex numbers is a powerful tool to have in your arsenal.