Write A Parabola Equation In Standard Form

Quick Links :

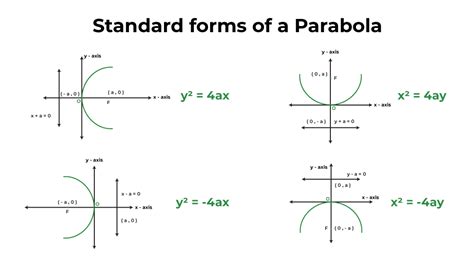
The parabola is one of the most fundamental concepts in mathematics, especially in the realm of algebra and geometry. A parabola is a type of quadratic curve that is U-shaped and has a single turning point, which is known as the vertex. Parabolas have numerous real-world applications, including physics, engineering, economics, and more.

Understanding the Parabola Equation

A parabola equation can be written in various forms, but the standard form is the most widely used and accepted. The standard form of a parabola equation is:

y = ax^2 + bx + c

where:

• a is the coefficient of the squared term (x^2)
• b is the coefficient of the linear term (x)
• c is the constant term

The values of a, b, and c determine the shape, size, and position of the parabola. For instance, if a is positive, the parabola opens upwards; if a is negative, the parabola opens downwards.

Breaking Down the Parabola Equation

To better understand the parabola equation, let's break it down into its components:

• The squared term (ax^2) determines the curvature of the parabola. If a is large, the parabola will be more curved; if a is small, the parabola will be less curved.
• The linear term (bx) determines the axis of symmetry of the parabola. The axis of symmetry is the vertical line that passes through the vertex of the parabola.
• The constant term (c) determines the y-intercept of the parabola, which is the point where the parabola intersects the y-axis.

Working with Parabola Equations

Parabola equations can be solved and manipulated in various ways, including:

• Factoring: Factoring a parabola equation involves expressing it as a product of two binomials.
• Graphing: Graphing a parabola equation involves plotting the curve on a coordinate plane.
• Solving quadratic equations: Solving a quadratic equation involves finding the values of x that make the equation true.

Practical Applications of Parabolas

Parabolas have numerous practical applications in various fields, including:

• Physics: Parabolas are used to model the trajectory of projectiles, such as the path of a thrown ball or the trajectory of a rocket.
• Engineering: Parabolas are used to design curves for roads, bridges, and other infrastructure.
• Economics: Parabolas are used to model the behavior of economic systems, such as the relationship between supply and demand.

Common Mistakes When Working with Parabolas

When working with parabolas, there are several common mistakes to avoid, including:

• Incorrectly identifying the vertex or axis of symmetry.
• Failing to factor or simplify the equation correctly.
• Not considering the units or context of the problem.

Conclusion

In conclusion, understanding the parabola equation in standard form is essential for working with quadratic curves. By breaking down the equation into its components and understanding its various applications, you can better appreciate the importance of parabolas in mathematics and real-world problems. Remember to avoid common mistakes when working with parabolas, and always consider the units and context of the problem.

We hope you've enjoyed this in-depth look at parabola equations! Do you have any questions or comments about this topic? Share your thoughts in the comments section below!