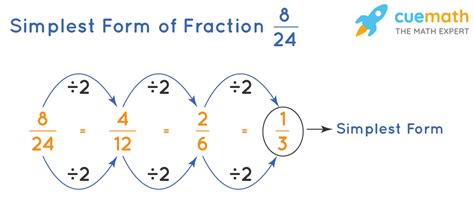
Reducing fractions to their simplest form is a fundamental concept in mathematics, and it's essential to understand the various methods to achieve this. One such fraction that can be simplified is 0.6. In this article, we'll explore three different ways to simplify 0.6 as a fraction.
The Importance of Simplifying Fractions
Simplifying fractions is crucial in mathematics, as it helps to reduce complex calculations and makes it easier to compare and add fractions. When fractions are in their simplest form, it's easier to identify equivalent ratios and make calculations more efficient.
Method 1: Converting Decimal to Fraction
One way to simplify 0.6 as a fraction is to convert the decimal to a fraction. To do this, we can write 0.6 as 6/10, as there are 6 tenths in 0.6.

By simplifying 6/10, we can divide both the numerator and denominator by 2, resulting in 3/5. Therefore, 0.6 as a simplified fraction is 3/5.
Method 2: Using Equivalent Ratios
Another way to simplify 0.6 as a fraction is to find an equivalent ratio. Since 0.6 is equal to 6/10, we can find an equivalent ratio by multiplying or dividing both the numerator and denominator by the same number.
For example, we can multiply both the numerator and denominator by 2, resulting in 12/20. However, we can simplify further by dividing both the numerator and denominator by 4, resulting in 3/5.

As we can see, using equivalent ratios also results in 0.6 being simplified to 3/5.
Method 3: Finding the Greatest Common Divisor (GCD)
A third way to simplify 0.6 as a fraction is to find the greatest common divisor (GCD) of the numerator and denominator. To do this, we can write 0.6 as 6/10 and find the GCD of 6 and 10.
The factors of 6 are 1, 2, 3, and 6, while the factors of 10 are 1, 2, 5, and 10. The greatest common factor of 6 and 10 is 2.

By dividing both the numerator and denominator by the GCD (2), we can simplify 6/10 to 3/5.
Conclusion
In this article, we've explored three different ways to simplify 0.6 as a fraction. Whether you use the decimal to fraction conversion method, equivalent ratios, or finding the GCD, the result is the same: 0.6 simplifies to 3/5. By understanding these methods, you can simplify fractions with ease and make calculations more efficient.
Why Simplifying Fractions is Important
Simplifying fractions is an essential concept in mathematics, and it's crucial to understand why it's important.
Efficient Calculations
Simplifying fractions makes calculations more efficient. When fractions are in their simplest form, it's easier to add, subtract, multiply, and divide them.
Comparing Fractions
Simplifying fractions also makes it easier to compare them. When fractions are in their simplest form, it's easier to identify equivalent ratios and compare their values.
Real-World Applications
Simplifying fractions has real-world applications in various fields, such as cooking, finance, and science. By understanding how to simplify fractions, you can make calculations more efficient and accurate.

We hope this article has helped you understand the importance of simplifying fractions and how to simplify 0.6 as a fraction using three different methods.
Get Involved!
Do you have any questions or comments about simplifying fractions? Share your thoughts with us in the comments section below. We'd love to hear from you!
What is the simplest form of 0.6 as a fraction?
+The simplest form of 0.6 as a fraction is 3/5.
Why is simplifying fractions important?
+Simplifying fractions is important because it makes calculations more efficient and accurate. It's also crucial for comparing fractions and has real-world applications in various fields.
How can I simplify a fraction?
+There are several ways to simplify a fraction, including converting decimals to fractions, using equivalent ratios, and finding the greatest common divisor (GCD).