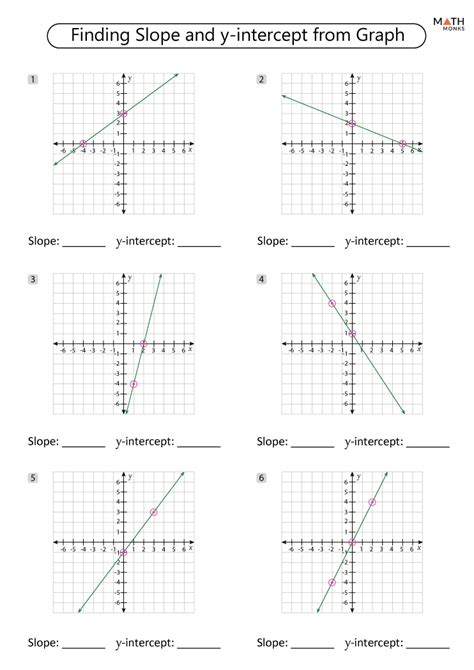
Mastering the slope-intercept form of a linear equation is a crucial skill for any student of mathematics, particularly those in algebra and geometry. The slope-intercept form, often denoted as y = mx + b, is a fundamental concept in understanding the relationship between the slope of a line and its y-intercept. This article will delve into five comprehensive ways to master the worksheet slope-intercept form, equipping you with the tools necessary to tackle problems with confidence.
Understanding the Basics

Before diving into more complex problems, it's essential to grasp the fundamental components of the slope-intercept form. The equation y = mx + b consists of three primary elements:
- m: The slope of the line, which indicates how steep the line is. A higher slope means a steeper line.
- b: The y-intercept, which is the point at which the line intersects the y-axis. This value remains constant for any given line.
- x: The independent variable, often representing the horizontal axis in a coordinate system.
Breaking Down the Equation
To effectively work with the slope-intercept form, you need to understand how to identify and manipulate the slope (m) and the y-intercept (b). This involves:
- Identifying the slope from a given equation or graph
- Calculating the y-intercept when the slope and a point on the line are known
- Graphing lines using the slope-intercept form
Method 1: Graphical Approach

One of the most intuitive ways to understand the slope-intercept form is through graphing. By plotting the y-intercept and using the slope to determine the rise over run, you can visually represent the line. This method is particularly useful for:
- Visualizing the relationship between the slope and the line's steepness
- Identifying the y-intercept and its significance in the equation
Step-by-Step Graphing
- Plot the y-intercept on the graph.
- Use the slope to determine the rise (change in y) and run (change in x).
- From the y-intercept, move up or down by the rise and left or right by the run.
- Draw the line through the new point.
Method 2: Algebraic Manipulation

Algebraic manipulation involves working with the equation y = mx + b to solve for unknown variables. This method is useful for:
- Finding the slope when given the y-intercept and another point on the line
- Determining the y-intercept when the slope and a point are known
Example Problem
Given the equation y = 2x + 3, find the y-intercept.
- The y-intercept is the value of b, which is 3.
Method 3: Real-World Applications

Applying the slope-intercept form to real-world problems can make the concept more tangible and interesting. Examples include:
- Modeling population growth or decline
- Analyzing the cost of goods or services
- Understanding the relationship between distance and time in physics
Example Problem
A company sells two products, A and B. The cost of product A is $5 per unit, and the fixed cost is $10. The cost of product B is $3 per unit, with a fixed cost of $15. Which product is more cost-effective for large orders?
- Product A: y = 5x + 10
- Product B: y = 3x + 15
- Comparing the slopes (5 and 3), product B is more cost-effective for large orders.
Method 4: Practice with Worksheets

Practicing with worksheets is an essential part of mastering the slope-intercept form. This method allows you to:
- Apply theoretical knowledge to practical problems
- Develop problem-solving skills and speed
- Identify and address any knowledge gaps
Tips for Effective Practice
- Start with simple problems and gradually move to more complex ones.
- Focus on understanding the underlying concepts rather than just solving the problems.
- Use online resources or worksheets with answers to check your work.
Method 5: Collaborative Learning

Collaborative learning involves working with peers or a study group to master the slope-intercept form. This method is useful for:
- Discussing and clarifying concepts
- Sharing knowledge and resources
- Developing teamwork and communication skills
Tips for Effective Collaboration
- Join a study group or find a study partner.
- Share and discuss worksheets and problems.
- Encourage active participation and feedback.
What is the slope-intercept form of a linear equation?
+The slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.
How do I graph a line using the slope-intercept form?
+Plot the y-intercept, use the slope to determine the rise and run, and draw the line through the new point.
What are some real-world applications of the slope-intercept form?
+Examples include modeling population growth, analyzing costs, and understanding distance-time relationships in physics.
By incorporating these five methods into your learning routine, you'll be well on your way to mastering the worksheet slope-intercept form. Remember to practice consistently, apply theoretical knowledge to practical problems, and collaborate with peers to reinforce your understanding. With dedication and persistence, you'll become proficient in working with the slope-intercept form and be able to tackle even the most challenging problems with confidence.