Linear equations are a fundamental concept in mathematics, and graphing them is an essential skill for anyone looking to understand and work with linear relationships. One of the most common forms of linear equations is the slope-intercept form, which provides a straightforward way to graph linear equations. In this article, we will explore the concept of slope-intercept form and provide a step-by-step guide on how to graph linear equations using this form.
Understanding Slope-Intercept Form
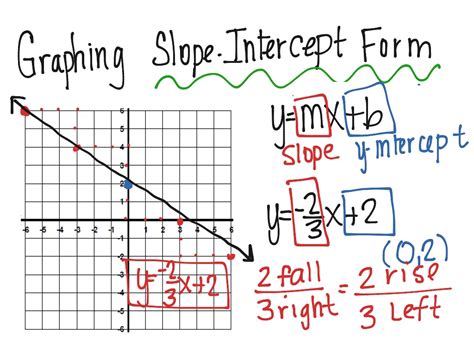
The slope-intercept form of a linear equation is given by the equation y = mx + b, where m represents the slope of the line and b represents the y-intercept. The slope (m) tells us how steep the line is, while the y-intercept (b) tells us where the line crosses the y-axis.

Benefits of Using Slope-Intercept Form
Using slope-intercept form to graph linear equations offers several benefits. For one, it allows us to easily identify the slope and y-intercept of the line, which can be useful in a variety of applications. Additionally, slope-intercept form makes it easy to graph linear equations by providing a clear and concise way to represent the line.
Step-by-Step Guide to Graphing Linear Equations Using Slope-Intercept Form
Graphing linear equations using slope-intercept form is a straightforward process that involves just a few steps. Here's a step-by-step guide to get you started:
Step 1: Write the Equation in Slope-Intercept Form
The first step is to write the linear equation in slope-intercept form. This means rearranging the equation to isolate y on one side of the equation.
Step 2: Identify the Slope and Y-Intercept
Once the equation is in slope-intercept form, identify the slope (m) and y-intercept (b). The slope will tell you how steep the line is, while the y-intercept will tell you where the line crosses the y-axis.
Step 3: Plot the Y-Intercept
Plot the y-intercept on the graph by marking a point on the y-axis at the value of b.
Step 4: Use the Slope to Plot Additional Points
Use the slope to plot additional points on the graph. To do this, start at the y-intercept and move up or down by the value of m, then move one unit to the right.
Step 5: Draw the Line
Once you have plotted several points, draw a line through them to create the graph of the linear equation.

Example Problems
Let's take a look at a few example problems to illustrate the process of graphing linear equations using slope-intercept form.
Example 1
Graph the linear equation y = 2x + 1.
Solution
To graph this equation, we first identify the slope and y-intercept. The slope is 2, and the y-intercept is 1. We plot the y-intercept on the graph, then use the slope to plot additional points. Starting at the y-intercept, we move up 2 units, then one unit to the right. We repeat this process to plot several points, then draw a line through them to create the graph.
Example 2
Graph the linear equation y = -3x - 2.
Solution
To graph this equation, we first identify the slope and y-intercept. The slope is -3, and the y-intercept is -2. We plot the y-intercept on the graph, then use the slope to plot additional points. Starting at the y-intercept, we move down 3 units, then one unit to the right. We repeat this process to plot several points, then draw a line through them to create the graph.
Tips and Tricks
Here are a few tips and tricks to keep in mind when graphing linear equations using slope-intercept form:
- Make sure to label the x and y axes on your graph.
- Use a ruler or straightedge to draw the line.
- Check your work by plugging in values of x and y to make sure they satisfy the equation.
Common Mistakes to Avoid
Here are a few common mistakes to avoid when graphing linear equations using slope-intercept form:
- Make sure to identify the slope and y-intercept correctly.
- Don't forget to plot the y-intercept on the graph.
- Use the slope to plot additional points, rather than just guessing.
Real-World Applications
Graphing linear equations using slope-intercept form has a variety of real-world applications. For example, it can be used to model population growth, investment returns, and more.
Conclusion: Take Action
Now that you've learned how to graph linear equations using slope-intercept form, it's time to take action. Practice graphing linear equations using this form, and see how it can help you in your studies or career.
Take the Next Step
What do you think is the most challenging part of graphing linear equations using slope-intercept form? Share your thoughts in the comments below.