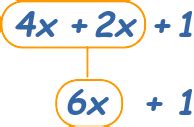The world of algebra can be daunting, especially when it comes to simplifying complex expressions. However, with the right techniques and strategies, anyone can master the art of simplifying algebra. In this article, we will delve into the world of algebra and explore the different ways to simplify expressions, making it easier for you to understand and work with them.
Understanding Algebraic Expressions

Before we dive into simplifying algebra, it's essential to understand what algebraic expressions are. An algebraic expression is a mathematical expression that consists of variables, constants, and mathematical operations. These expressions can be simple or complex, and they can be used to represent a wide range of mathematical concepts.
For example, the expression 2x + 3 is an algebraic expression that consists of a variable (x), a constant (3), and a mathematical operation (addition).
The Importance of Simplifying Algebra

Simplifying algebra is crucial in mathematics, as it allows us to work with complex expressions more efficiently. By simplifying algebraic expressions, we can:
- Make calculations easier and faster
- Identify patterns and relationships between variables
- Solve equations and inequalities more effectively
- Model real-world problems and make predictions
Basic Rules of Simplifying Algebra
To simplify algebraic expressions, we need to follow some basic rules. These rules include:
- Combining like terms: Combine terms that have the same variable and coefficient.
- Distributive property: Distribute a single term to multiple terms inside parentheses.
- Factoring out common factors: Factor out common factors from multiple terms.
Simplifying Linear Expressions

Linear expressions are algebraic expressions that consist of a single term or a sum of terms, where each term has a variable and a coefficient. To simplify linear expressions, we can combine like terms and factor out common factors.
For example, the expression 2x + 3x can be simplified by combining like terms: 5x.
Examples of Simplifying Linear Expressions
- Simplify the expression: 2x + 3x Answer: 5x
- Simplify the expression: x + 2x Answer: 3x
- Simplify the expression: 3x - 2x Answer: x
Simplifying Quadratic Expressions

Quadratic expressions are algebraic expressions that consist of a squared variable and a constant term. To simplify quadratic expressions, we can factor out common factors and use the distributive property.
For example, the expression x^2 + 4x + 4 can be simplified by factoring out a common factor: (x + 2)^2.
Examples of Simplifying Quadratic Expressions
- Simplify the expression: x^2 + 4x + 4 Answer: (x + 2)^2
- Simplify the expression: x^2 - 4x + 4 Answer: (x - 2)^2
- Simplify the expression: x^2 + 2x + 1 Answer: (x + 1)^2
Simplifying Rational Expressions

Rational expressions are algebraic expressions that consist of a fraction with variables and constants. To simplify rational expressions, we can factor out common factors and cancel out common terms.
For example, the expression (x + 1)/(x - 1) can be simplified by factoring out a common factor: (x + 1)/(x - 1) = (x + 1)/(x - 1) * (x + 1)/(x + 1) = (x + 1)^2/(x^2 - 1).
Examples of Simplifying Rational Expressions
- Simplify the expression: (x + 1)/(x - 1) Answer: (x + 1)^2/(x^2 - 1)
- Simplify the expression: (x^2 + 1)/(x^2 - 1) Answer: (x^2 + 1)/(x^2 - 1) * (x^2 + 1)/(x^2 + 1) = (x^2 + 1)^2/(x^4 - 1)
- Simplify the expression: (x^2 - 1)/(x^2 + 1) Answer: (x^2 - 1)/(x^2 + 1) * (x^2 - 1)/(x^2 - 1) = (x^2 - 1)^2/(x^4 - 1)
Conclusion: Mastering the Art of Simplifying Algebra

Simplifying algebra is an essential skill in mathematics, and with practice and patience, anyone can master it. By understanding the basic rules of simplifying algebra and applying them to different types of expressions, you can become proficient in simplifying algebraic expressions.
We hope this article has helped you understand the concept of simplifying algebra and provided you with the tools and techniques to simplify complex expressions. Remember to practice regularly and apply these techniques to different types of expressions to become proficient in simplifying algebra.
We encourage you to share your thoughts and feedback on this article in the comments section below. If you have any questions or need further clarification on any of the concepts discussed in this article, please don't hesitate to ask.
What is algebraic expression?
+An algebraic expression is a mathematical expression that consists of variables, constants, and mathematical operations.
Why is simplifying algebra important?
+Simplifying algebra is important because it allows us to work with complex expressions more efficiently, make calculations easier and faster, identify patterns and relationships between variables, and solve equations and inequalities more effectively.
What are the basic rules of simplifying algebra?
+The basic rules of simplifying algebra include combining like terms, distributive property, and factoring out common factors.