Simplify Radical Expressions In 1 Easy Step

Radical expressions can be intimidating, especially when they contain multiple terms or variables. However, with a simple trick, you can simplify radical expressions in just one easy step. In this article, we'll explore the concept of radical expressions, the importance of simplifying them, and the easy step to simplify them.
Radical expressions are mathematical expressions that contain a radical sign (√). They are used to represent the nth root of a number, where n is a positive integer. Radical expressions can be simple, like √16, or complex, like √(x^2 + y^2). Simplifying radical expressions is essential in algebra, geometry, and other branches of mathematics, as it helps to make calculations easier and more manageable.
Why Simplify Radical Expressions?
Simplifying radical expressions is crucial in various mathematical operations, such as adding, subtracting, multiplying, and dividing. When radical expressions are simplified, they become easier to manipulate and solve. Simplified radical expressions also help to avoid errors and confusion, especially when working with complex equations or formulas.
The 1 Easy Step to Simplify Radical Expressions

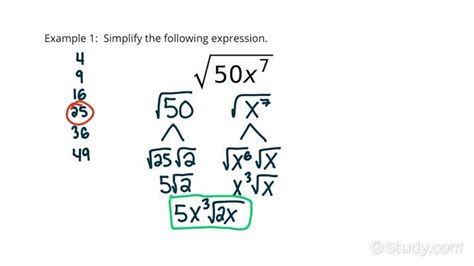
The one easy step to simplify radical expressions is to factor out the perfect squares. A perfect square is a number that can be expressed as the square of an integer, such as 16 (4^2) or 25 (5^2). When you factor out the perfect squares from a radical expression, you can simplify it by taking the square root of the perfect square.
For example, consider the radical expression √(16x^2). To simplify this expression, you can factor out the perfect square 16, which is equal to 4^2. This gives you √(4^2x^2). Now, you can take the square root of the perfect square 4^2, which is 4. This leaves you with 4x, which is the simplified form of the original radical expression.
Examples of Simplifying Radical Expressions
Here are some more examples of simplifying radical expressions using the one easy step:
- √(25x^2) = √(5^2x^2) = 5x
- √(36y^2) = √(6^2y^2) = 6y
- √(49z^2) = √(7^2z^2) = 7z
Benefits of Simplifying Radical Expressions

Simplifying radical expressions has several benefits, including:
- Easier calculations: Simplified radical expressions make calculations easier and faster.
- Reduced errors: Simplified radical expressions reduce the risk of errors and confusion.
- Improved understanding: Simplified radical expressions help to improve understanding of mathematical concepts and relationships.
Common Mistakes to Avoid When Simplifying Radical Expressions
When simplifying radical expressions, it's essential to avoid common mistakes, such as:
- Forgetting to factor out perfect squares
- Taking the square root of a non-perfect square
- Simplifying expressions that are not radical expressions
Real-World Applications of Simplifying Radical Expressions

Simplifying radical expressions has several real-world applications, including:
- Physics: Simplified radical expressions are used to describe the motion of objects and the forces that act upon them.
- Engineering: Simplified radical expressions are used to design and optimize systems, such as bridges and buildings.
- Computer Science: Simplified radical expressions are used in algorithms and data structures.
Conclusion and Next Steps
In conclusion, simplifying radical expressions is an essential skill in mathematics, and it can be achieved in just one easy step. By factoring out perfect squares, you can simplify radical expressions and make calculations easier and more manageable. To improve your skills in simplifying radical expressions, practice with different examples and exercises. You can also explore real-world applications of simplified radical expressions in various fields, such as physics, engineering, and computer science.
What's Next?
Now that you've learned the one easy step to simplify radical expressions, you can take your skills to the next level by exploring more advanced topics, such as:
- Simplifying radical expressions with variables
- Simplifying radical expressions with multiple terms
- Using simplified radical expressions in equations and formulas
Stay tuned for more articles and resources on mathematics and science!
What is a radical expression?
+A radical expression is a mathematical expression that contains a radical sign (√). It is used to represent the nth root of a number, where n is a positive integer.
Why is it important to simplify radical expressions?
+Simplifying radical expressions is essential in various mathematical operations, such as adding, subtracting, multiplying, and dividing. It helps to make calculations easier and more manageable, and it reduces the risk of errors and confusion.
What is the one easy step to simplify radical expressions?
+The one easy step to simplify radical expressions is to factor out the perfect squares. This involves factoring out numbers that can be expressed as the square of an integer, such as 16 (4^2) or 25 (5^2).