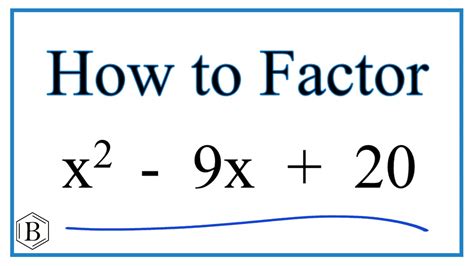Understanding Quadratic Equations and Factoring

Quadratic equations are a fundamental concept in algebra, and factoring is a crucial technique used to solve them. A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable is two. The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. In this article, we will focus on factoring a specific quadratic equation, x^2 + 9x + 20.
The Importance of Factoring Quadratic Equations
Factoring quadratic equations is essential in algebra because it allows us to find the roots or solutions of the equation. By factoring, we can rewrite the quadratic equation in a product form, which makes it easier to solve. Factoring also helps us to identify the x-intercepts of the quadratic function, which are critical in graphing and analyzing the function's behavior.
Step 1: Identify the Factors of the Constant Term

To factor the quadratic equation x^2 + 9x + 20, we need to find two numbers whose product is 20 and whose sum is 9. These numbers are 4 and 5, since 4 × 5 = 20 and 4 + 5 = 9. We can write the equation as (x + 4)(x + 5) = 0.
Why This Step Is Crucial
Identifying the factors of the constant term is crucial in factoring quadratic equations. By finding the correct factors, we can rewrite the equation in a product form, which allows us to solve for the roots of the equation. In this case, the factors 4 and 5 help us to rewrite the equation as (x + 4)(x + 5) = 0.
Step 2: Write the Factored Form of the Quadratic Equation

Now that we have identified the factors of the constant term, we can write the factored form of the quadratic equation. The factored form of x^2 + 9x + 20 is (x + 4)(x + 5) = 0.
Benefits of the Factored Form
The factored form of the quadratic equation provides several benefits. It allows us to easily identify the roots of the equation, which are x = -4 and x = -5. The factored form also helps us to graph the quadratic function and analyze its behavior.
Conclusion and Next Steps

In conclusion, factoring quadratic equations is a crucial technique in algebra. By following the two easy steps outlined in this article, you can factor quadratic equations with ease. Remember to identify the factors of the constant term and write the factored form of the quadratic equation.
Take Your Learning to the Next Level
Now that you have mastered factoring quadratic equations, it's time to take your learning to the next level. Practice factoring different types of quadratic equations, and explore other algebraic techniques, such as solving linear equations and graphing functions.
What is the general form of a quadratic equation?
+The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable.
Why is factoring quadratic equations important?
+Factoring quadratic equations is important because it allows us to find the roots or solutions of the equation, which is essential in algebra and other areas of mathematics.
What are the benefits of the factored form of a quadratic equation?
+The factored form of a quadratic equation provides several benefits, including easily identifying the roots of the equation and analyzing the behavior of the quadratic function.