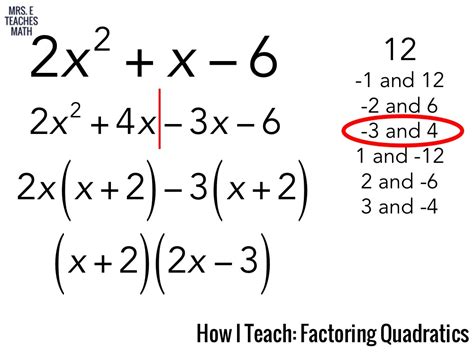Factoring quadratic expressions is a fundamental concept in algebra, and it's essential to understand the methods and techniques involved. In this article, we'll explore the factoring of quadratic expressions, specifically Q² + 12q + 36.
Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, which means the highest power of the variable (in this case, Q) is two. The general form of a quadratic expression is ax² + bx + c, where a, b, and c are constants. In our case, the quadratic expression is Q² + 12q + 36.

Factoring Quadratic Expressions
Factoring a quadratic expression involves expressing it as a product of two binomials. There are several methods to factor quadratic expressions, including:
- Factoring by grouping
- Factoring by using the perfect square trinomial formula
- Factoring by using the quadratic formula
In this article, we'll focus on factoring by using the perfect square trinomial formula.
The Perfect Square Trinomial Formula
The perfect square trinomial formula is a² + 2ab + b² = (a + b)². This formula allows us to factor quadratic expressions in the form of a perfect square trinomial.

Applying the Perfect Square Trinomial Formula
To factor Q² + 12q + 36, we need to identify the values of a and b in the perfect square trinomial formula. Comparing the quadratic expression to the formula, we can see that a = Q and b = 6.
Using the formula, we can rewrite the quadratic expression as:
Q² + 12q + 36 = (Q + 6)²
Therefore, the factored form of Q² + 12q + 36 is (Q + 6)².
Benefits of Factoring Quadratic Expressions
Factoring quadratic expressions has several benefits, including:
- Simplifying complex expressions
- Solving quadratic equations
- Finding the roots of quadratic equations
- Graphing quadratic functions
By factoring quadratic expressions, we can gain a deeper understanding of the underlying structure of the expression and make it easier to work with.

Real-World Applications of Factoring Quadratic Expressions
Factoring quadratic expressions has numerous real-world applications, including:
- Physics and engineering: Quadratic equations are used to model the motion of objects and optimize systems.
- Computer science: Quadratic equations are used in algorithms for computer graphics and game development.
- Economics: Quadratic equations are used to model economic systems and make predictions about market trends.
By understanding how to factor quadratic expressions, we can develop problem-solving skills and apply mathematical concepts to real-world problems.
Common Mistakes to Avoid
When factoring quadratic expressions, it's essential to avoid common mistakes, including:
- Incorrectly identifying the values of a and b
- Forgetting to include the constant term
- Not simplifying the expression fully
By being aware of these common mistakes, we can ensure that our factoring is accurate and complete.

Conclusion and Final Thoughts
In conclusion, factoring quadratic expressions is a fundamental concept in algebra that requires practice and patience. By understanding the perfect square trinomial formula and applying it to quadratic expressions like Q² + 12q + 36, we can develop problem-solving skills and apply mathematical concepts to real-world problems.
We encourage you to share your thoughts and questions about factoring quadratic expressions in the comments below. Don't forget to share this article with your friends and colleagues who may benefit from it!
What is the difference between a quadratic expression and a quadratic equation?
+A quadratic expression is a polynomial of degree two, while a quadratic equation is a statement that sets a quadratic expression equal to zero.
What is the perfect square trinomial formula?
+The perfect square trinomial formula is a² + 2ab + b² = (a + b)².
What are the benefits of factoring quadratic expressions?
+Factoring quadratic expressions simplifies complex expressions, solves quadratic equations, finds the roots of quadratic equations, and graphs quadratic functions.