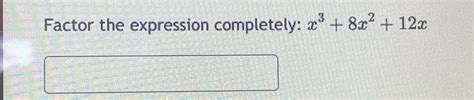
When it comes to factoring algebraic expressions, many students find it daunting. However, with a clear understanding of the concepts and a step-by-step approach, factoring can become a manageable task. In this article, we'll focus on factoring the expression 8x2 + 12x, breaking down the process into simple and easy-to-follow steps.
Understanding the Basics of Factoring

Before diving into the expression 8x2 + 12x, it's essential to understand the basics of factoring. Factoring involves expressing an algebraic expression as a product of simpler expressions, called factors. The goal is to find the common factors among the terms and combine them in a way that simplifies the expression.
Identifying the Greatest Common Factor (GCF)

The first step in factoring 8x2 + 12x is to identify the greatest common factor (GCF) of the two terms. The GCF is the largest expression that divides both terms evenly. In this case, the GCF of 8x2 and 12x is 4x.
How to Find the GCF
To find the GCF, list the factors of each term:
- Factors of 8x2: 1, 2, 4, 8, x, 2x, 4x, 8x2
- Factors of 12x: 1, 2, 3, 4, 6, 12, x, 2x, 3x, 4x, 6x, 12x
The common factors are 1, 2, and 4x. The greatest common factor is 4x.
Factoring Out the GCF

Now that we've identified the GCF, we can factor it out of the expression. To do this, divide each term by the GCF and write the result as a product:
8x2 + 12x = 4x(2x + 3)
Why Factoring Out the GCF Works
Factoring out the GCF works because it allows us to combine like terms and simplify the expression. When we divide each term by the GCF, we're essentially removing the common factor and leaving behind a simpler expression.
Factoring Out the Remaining Terms

Now that we've factored out the GCF, we can focus on the remaining terms. In this case, the remaining terms are 2x + 3.
Factoring the Remaining Terms
The remaining terms 2x + 3 cannot be factored further. However, we can rewrite the expression as:
4x(2x + 3)
This is the final factored form of the expression 8x2 + 12x.
Real-World Applications of Factoring

Factoring is not just a theoretical concept; it has numerous real-world applications. For instance, factoring is used in:
- Physics to simplify complex equations
- Engineering to optimize system design
- Computer science to develop algorithms
- Economics to model market trends
Common Mistakes to Avoid When Factoring

When factoring, it's essential to avoid common mistakes. Here are a few:
- Forgetting to identify the GCF
- Factoring out the wrong terms
- Not simplifying the expression fully
Conclusion

In conclusion, factoring the expression 8x2 + 12x involves identifying the GCF, factoring it out, and simplifying the remaining terms. By following these steps and avoiding common mistakes, you can become proficient in factoring and tackle more complex expressions.
We hope this article has helped you understand the process of factoring and has provided you with the confidence to tackle algebraic expressions. If you have any questions or need further clarification, please don't hesitate to ask.
What is the greatest common factor (GCF) of 8x2 and 12x?
+The GCF of 8x2 and 12x is 4x.
How do I factor out the GCF from an expression?
+To factor out the GCF, divide each term by the GCF and write the result as a product.
What are some real-world applications of factoring?
+Factoring has numerous real-world applications, including physics, engineering, computer science, and economics.