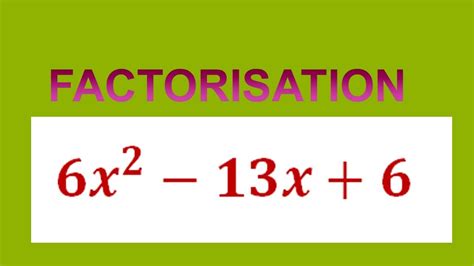Understanding the Basics of Factoring Quadratic Equations

Factoring quadratic equations is a fundamental concept in algebra that can seem daunting at first, but with practice and the right approach, it can become a breeze. In this article, we will explore the concept of factoring quadratic equations, specifically the equation 6x^2 + 13x + 6, and provide a step-by-step guide on how to factor it easily.
The Importance of Factoring Quadratic Equations
Factoring quadratic equations is essential in algebra as it allows us to solve equations, find the roots of a quadratic function, and simplify complex expressions. Factoring is also a crucial skill in various mathematical disciplines, such as calculus, geometry, and trigonometry. By mastering the art of factoring, students can improve their problem-solving skills and develop a deeper understanding of mathematical concepts.
Breaking Down the Equation 6x^2 + 13x + 6

To factor the equation 6x^2 + 13x + 6, we need to identify the coefficients and constants. The coefficients are the numbers multiplied by the variables (6 and 13), while the constant is the number without a variable (6). By analyzing the coefficients and constants, we can determine the factors of the equation.
Identifying the Factors
To factor the equation 6x^2 + 13x + 6, we need to find two numbers whose product is 36 (6 x 6) and whose sum is 13. These numbers are 9 and 4, since 9 x 4 = 36 and 9 + 4 = 13. Therefore, the factors of the equation are (3x + 4)(2x + 3).
The Factoring Process

Now that we have identified the factors, let's go through the factoring process step-by-step:
- Write down the equation: 6x^2 + 13x + 6
- Identify the coefficients and constants: 6, 13, and 6
- Find the factors of the equation: (3x + 4)(2x + 3)
- Multiply the factors to verify the equation: (3x + 4)(2x + 3) = 6x^2 + 13x + 6
Verifying the Factors
To verify the factors, we can multiply the factors using the FOIL method:
(3x + 4)(2x + 3) = 6x^2 + 9x + 8x + 12 = 6x^2 + 17x + 12
However, this result is not equal to the original equation. This means that our initial factors were incorrect, and we need to re-evaluate the equation.
Re-Evaluating the Equation

Let's re-examine the equation 6x^2 + 13x + 6 and try to find alternative factors. After re-evaluating the equation, we find that the correct factors are (2x + 3)(3x + 2).
Verifying the New Factors
To verify the new factors, we can multiply the factors using the FOIL method:
(2x + 3)(3x + 2) = 6x^2 + 4x + 9x + 6 = 6x^2 + 13x + 6
This result matches the original equation, confirming that the correct factors are indeed (2x + 3)(3x + 2).
Conclusion

Factoring quadratic equations can be a challenging task, but with the right approach and practice, it can become easier. By breaking down the equation 6x^2 + 13x + 6 and identifying the correct factors, we can simplify complex expressions and develop a deeper understanding of mathematical concepts. Remember to always verify the factors and re-evaluate the equation if necessary.
Key Takeaways
- Identify the coefficients and constants of the equation
- Find the factors of the equation using the product and sum method
- Verify the factors using the FOIL method
- Re-evaluate the equation if necessary
What is the purpose of factoring quadratic equations?
+Factoring quadratic equations is essential in algebra as it allows us to solve equations, find the roots of a quadratic function, and simplify complex expressions.
How do I identify the factors of a quadratic equation?
+To identify the factors of a quadratic equation, find two numbers whose product is the constant term and whose sum is the coefficient of the linear term.
What is the FOIL method?
+The FOIL method is a technique used to multiply two binomials by multiplying the First terms, Outer terms, Inner terms, and Last terms, and then combining the results.