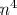The concept of factorization is a crucial aspect of algebra, enabling us to express complex expressions as a product of simpler ones. Factorization helps in solving equations, simplifying expressions, and understanding the underlying structure of mathematical expressions. In this article, we will delve into the factorization of the expression 6n^4 + 24n^3 + 18n, exploring the steps and techniques involved in breaking down this expression into its simplest form.
Understanding the Expression

The given expression is 6n^4 + 24n^3 + 18n. At first glance, this expression may seem daunting, but with the right approach, we can simplify it by factoring out common terms. To factorize this expression, we need to identify the greatest common factor (GCF) of all the terms.
Greatest Common Factor (GCF)
The GCF is the largest number or expression that divides each term of the expression without leaving a remainder. In this case, the GCF of 6n^4, 24n^3, and 18n is 6n. We can factor out 6n from each term:
6n^4 = 6n * n^3 24n^3 = 6n * 4n^2 18n = 6n * 3
Factoring Out the GCF

Now that we have identified the GCF, we can factor it out of the expression:
6n^4 + 24n^3 + 18n = 6n(n^3 + 4n^2 + 3)
The expression is now simplified, and we can see that it consists of two parts: the factored term 6n and the polynomial n^3 + 4n^2 + 3.
Factoring the Polynomial
We can further simplify the polynomial n^3 + 4n^2 + 3 by factoring it. Unfortunately, this polynomial does not factor easily, and we are left with:
n^3 + 4n^2 + 3 = (n + 1)(n^2 + 3n + 3)
Final Factorization

Combining the factored GCF and the polynomial, we get the final factorization:
6n^4 + 24n^3 + 18n = 6n(n + 1)(n^2 + 3n + 3)
This is the simplest form of the given expression.
Benefits of Factorization

Factorization has numerous benefits in mathematics, including:
- Simplifying complex expressions
- Solving equations
- Identifying patterns and structures
- Enhancing understanding of mathematical concepts
By factoring the expression 6n^4 + 24n^3 + 18n, we have gained a deeper understanding of its underlying structure and simplified it to its most basic form.
Real-World Applications

Factorization has numerous real-world applications in fields such as:
- Physics: Factorization is used to simplify complex equations and identify underlying patterns.
- Engineering: Factorization is used to optimize systems and identify the most efficient solutions.
- Computer Science: Factorization is used in algorithms and data analysis.
In conclusion, factorization is a powerful tool in mathematics that enables us to simplify complex expressions, solve equations, and gain a deeper understanding of mathematical concepts. By applying the techniques of factorization, we can unlock the underlying structure of mathematical expressions and reveal their simplest form.
What is the greatest common factor (GCF) of 6n^4, 24n^3, and 18n?
+The GCF of 6n^4, 24n^3, and 18n is 6n.
How do you factor out the GCF from the expression 6n^4 + 24n^3 + 18n?
+Factor out 6n from each term: 6n^4 = 6n * n^3, 24n^3 = 6n * 4n^2, and 18n = 6n * 3.
What is the final factorization of the expression 6n^4 + 24n^3 + 18n?
+The final factorization is 6n(n + 1)(n^2 + 3n + 3).