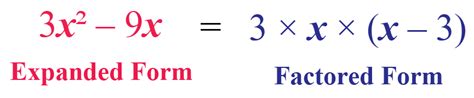Expression In Factored Form Explained

Quick Links :

Algebra is a fundamental branch of mathematics that deals with variables and their relationships. One of the most important concepts in algebra is factoring, which involves expressing an algebraic expression as a product of simpler expressions. In this article, we will explore the concept of expression in factored form, its importance, and how to factor different types of expressions.

What is Expression in Factored Form?

An expression in factored form is a mathematical expression that is written as a product of simpler expressions, called factors. Factoring involves finding the factors of an expression and writing it in a form that shows these factors clearly. For example, the expression x^2 + 5x + 6 can be factored as (x + 2)(x + 3). This factored form shows that the original expression can be broken down into two simpler expressions, (x + 2) and (x + 3), which are multiplied together.

Why is Expression in Factored Form Important?

Expression in factored form is important for several reasons:

• Simplifies complex expressions: Factoring helps to simplify complex expressions by breaking them down into simpler components.
• Makes it easier to solve equations: Factored form makes it easier to solve equations by allowing us to work with simpler expressions.
• Helps in graphing: Factored form is useful in graphing functions, as it allows us to identify the x-intercepts and other important features of the graph.
• Used in calculus: Factored form is used in calculus to find the derivative and integral of functions.

Types of Factoring

There are several types of factoring, including:

• GCF factoring: This involves factoring out the greatest common factor (GCF) of an expression.
• Difference of squares factoring: This involves factoring expressions of the form a^2 - b^2.
• Sum and difference of cubes factoring: This involves factoring expressions of the form a^3 + b^3 or a^3 - b^3.
• Factoring by grouping: This involves factoring expressions by grouping terms and factoring out common factors.

How to Factor Expressions

Factoring expressions involves finding the factors of an expression and writing it in factored form. Here are some steps to follow:

1. Look for common factors: Look for common factors among the terms of the expression.
2. Check for difference of squares: Check if the expression is in the form a^2 - b^2.
3. Check for sum and difference of cubes: Check if the expression is in the form a^3 + b^3 or a^3 - b^3.
4. Group terms: Group terms that have common factors.
5. Factor out common factors: Factor out common factors from each group.

Examples of Factoring

Here are some examples of factoring:

• GCF factoring: 6x^2 + 12x = 6(x^2 + 2x)
• Difference of squares factoring: x^2 - 4 = (x + 2)(x - 2)
• Sum and difference of cubes factoring: x^3 + 8 = (x + 2)(x^2 - 2x + 4)
• Factoring by grouping: x^2 + 5x + 6 = (x + 2)(x + 3)

Common Mistakes in Factoring

Here are some common mistakes to avoid when factoring:

• Not checking for common factors: Not checking for common factors among the terms of the expression.
• Not checking for difference of squares: Not checking if the expression is in the form a^2 - b^2.
• Not grouping terms correctly: Not grouping terms correctly, which can lead to incorrect factoring.
• Not factoring out common factors: Not factoring out common factors from each group.

Conclusion

In conclusion, expression in factored form is an important concept in algebra that involves expressing an expression as a product of simpler expressions. Factoring helps to simplify complex expressions, makes it easier to solve equations, and is used in calculus. There are several types of factoring, including GCF factoring, difference of squares factoring, sum and difference of cubes factoring, and factoring by grouping. By following the steps outlined in this article and avoiding common mistakes, you can become proficient in factoring expressions.

We hope this article has helped you understand the concept of expression in factored form. Do you have any questions or need further clarification? Please leave a comment below.