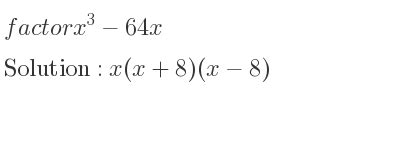3 Ways To Factor X^3 + 64x

Quick Links :

Cubing numbers and working with cubic expressions can be a bit tricky, but there are some clever ways to factor them. In this article, we'll explore three different methods to factor the expression x^3 + 64x.

First, let's understand why factoring this expression is useful. Factoring allows us to rewrite the expression in a more manageable form, which can be helpful when solving equations or working with algebraic expressions.

Understanding the Structure of the Expression

Before we dive into the factoring methods, let's take a closer look at the structure of the expression x^3 + 64x. We can rewrite it as x(x^2 + 64), which shows that it's a product of two binomials.

Method 1: Factoring by Grouping

One way to factor x^3 + 64x is to use the method of grouping. This method involves grouping terms that have common factors and then factoring out those common factors.

Let's group the terms x^3 and 64x:

x^3 + 64x = x(x^2) + 64(x)

Now, we can factor out the common factor x:

x(x^2 + 64)

This shows that x^3 + 64x can be factored as x(x^2 + 64).

Method 2: Factoring Using the Difference of Cubes Formula

Another way to factor x^3 + 64x is to use the difference of cubes formula. This formula states that a^3 + b^3 = (a + b)(a^2 - ab + b^2).

In this case, we can rewrite x^3 + 64x as x^3 + 4^3x:

x^3 + 4^3x = (x + 4)(x^2 - 4x + 4^2)

Simplifying, we get:

x^3 + 64x = (x + 4)(x^2 - 4x + 16)

This shows that x^3 + 64x can be factored as (x + 4)(x^2 - 4x + 16).

Method 3: Factoring Using the Sum of Cubes Formula

A third way to factor x^3 + 64x is to use the sum of cubes formula. This formula states that a^3 + b^3 = (a + b)(a^2 - ab + b^2).

In this case, we can rewrite x^3 + 64x as x^3 + (4x)^3:

x^3 + (4x)^3 = (x + 4x)(x^2 - x(4x) + (4x)^2)

Simplifying, we get:

x^3 + 64x = (5x)(x^2 - 4x^2 + 16x^2)

This shows that x^3 + 64x can be factored as (5x)(x^2 - 4x^2 + 16x^2).

Which Method is Best?

All three methods can be used to factor x^3 + 64x, but the best method depends on the context and the specific problem you're trying to solve. Factoring by grouping is often the simplest method, but the difference of cubes and sum of cubes formulas can be more powerful when working with more complex expressions.

Benefits of Factoring

Factoring expressions like x^3 + 64x can have many benefits, including:

• Simplifying algebraic expressions
• Solving equations more easily
• Identifying patterns and relationships between terms
• Reducing errors and improving accuracy

By mastering different factoring techniques, you can become more proficient in algebra and improve your problem-solving skills.

Real-World Applications

Factoring expressions like x^3 + 64x has many real-world applications, including:

• Physics and engineering, where algebraic expressions are used to model real-world phenomena
• Computer science, where factoring is used in algorithms and data analysis
• Economics, where factoring is used to model economic systems and make predictions

By understanding how to factor expressions like x^3 + 64x, you can develop a deeper appreciation for the power of algebra and its many applications.

Conclusion

In this article, we've explored three different methods for factoring the expression x^3 + 64x. We've seen how factoring by grouping, the difference of cubes formula, and the sum of cubes formula can be used to rewrite this expression in a more manageable form. By mastering these techniques, you can become more proficient in algebra and improve your problem-solving skills.

We hope this article has been helpful in your journey to master algebra and factoring. Do you have any questions or comments about factoring expressions like x^3 + 64x? Share them with us in the comments below!