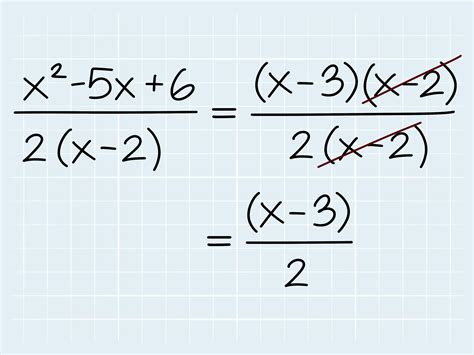Unlocking the Power of Factoring

Factoring expressions is a fundamental concept in mathematics that can simplify complex problems and reveal hidden patterns. In this article, we will explore the world of factoring and provide a step-by-step guide on how to simplify expressions using this powerful technique.
What is Factoring?

Factoring is the process of expressing an algebraic expression as a product of simpler expressions, called factors. It is a reverse operation of multiplication, where we break down a complex expression into its constituent parts. Factoring is used to solve equations, simplify expressions, and graph functions.
Why is Factoring Important?
Factoring is a crucial skill in mathematics, as it helps to:
- Simplify complex expressions and make them more manageable
- Solve equations and inequalities by factoring out common factors
- Graph functions and identify patterns and relationships
- Develop problem-solving strategies and critical thinking skills
4 Steps to Simplify the Expression

Now that we have explored the importance of factoring, let's dive into the step-by-step process of simplifying expressions using factoring.
Step 1: Factor Out the Greatest Common Factor (GCF)
The first step in factoring is to identify the greatest common factor (GCF) of the expression. The GCF is the largest factor that divides all the terms of the expression without leaving a remainder.
Example: Factor out the GCF from the expression 12x + 18
- Identify the GCF: 6
- Factor out the GCF: 6(2x + 3)
Step 2: Look for Common Binomial Factors
The next step is to look for common binomial factors, which are expressions of the form (a + b) or (a - b).
Example: Factor the expression x^2 + 5x + 6
- Look for common binomial factors: (x + 3)(x + 2)
- Factor the expression: (x + 3)(x + 2)
Step 3: Factor Quadratic Expressions
Quadratic expressions can be factored using the quadratic formula or by looking for two binomial factors.
Example: Factor the expression x^2 - 4x - 5
- Use the quadratic formula: x = (-b ± √(b^2 - 4ac)) / 2a
- Factor the expression: (x - 5)(x + 1)
Step 4: Check and Simplify
The final step is to check and simplify the factored expression.
Example: Factor the expression 9x^2 - 12x - 4
- Factor out the GCF: 9x^2 - 12x - 4 = (3x - 2)(3x + 2)
- Check and simplify: (3x - 2)(3x + 2) = 9x^2 - 4
Real-World Applications of Factoring

Factoring has numerous real-world applications in fields such as physics, engineering, economics, and computer science. Here are a few examples:
- Physics: Factoring is used to solve equations of motion and energy.
- Engineering: Factoring is used to design and optimize systems, such as bridges and electronic circuits.
- Economics: Factoring is used to model and analyze economic systems, such as supply and demand.
- Computer Science: Factoring is used in cryptography and coding theory.
Conclusion

In conclusion, factoring is a powerful technique that can simplify complex expressions and reveal hidden patterns. By following the 4 steps outlined in this article, you can master the art of factoring and unlock the secrets of algebraic expressions. Whether you are a student, teacher, or professional, factoring is an essential skill that can help you solve problems and achieve success in mathematics and beyond.
We hope this article has inspired you to explore the world of factoring and apply its principles to your everyday life. Share your thoughts and experiences with factoring in the comments below, and don't forget to share this article with your friends and colleagues.
What is the difference between factoring and simplifying?
+Factoring is the process of expressing an algebraic expression as a product of simpler expressions, while simplifying is the process of reducing an expression to its simplest form.
Can factoring be used to solve all types of equations?
+No, factoring cannot be used to solve all types of equations. However, it can be used to solve linear and quadratic equations, as well as some types of polynomial equations.
What are some common mistakes to avoid when factoring?
+Some common mistakes to avoid when factoring include forgetting to factor out the GCF, looking for common binomial factors that are not present, and factoring quadratic expressions incorrectly.