What Is Radical Form In Math

Quick Links :

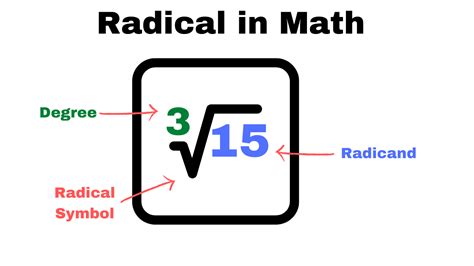
Radical form is a mathematical expression that represents a root of a number. It is a way to express a number as a root of another number, using a symbol called the radical sign (√). Radical form is used to simplify complex expressions and to solve equations involving roots.

Radical form has been a fundamental concept in mathematics for centuries, and it has numerous applications in various fields, including algebra, geometry, trigonometry, and calculus. In this article, we will explore the concept of radical form, its history, and its applications in mathematics.

History of Radical Form

The concept of radical form dates back to ancient civilizations, where mathematicians used geometric methods to calculate square roots and cube roots. The ancient Greeks, such as Pythagoras and Euclid, used radical form to solve equations involving roots.

The radical sign (√) was first introduced by the German mathematician Christoff Rudolff in the 16th century. Rudolff used the radical sign to represent the square root of a number. Later, the concept of radical form was extended to include cube roots, fourth roots, and higher-order roots.

Types of Radical Form

There are several types of radical form, including:

Simple Radical Form

Simple radical form is the most basic type of radical form. It is used to express a number as a root of another number. For example:

√16 = 4

In this example, the radical sign (√) is used to express the square root of 16, which is equal to 4.

Compound Radical Form

Compound radical form is used to express a number as a root of another number, where the radicand (the number inside the radical sign) is itself a radical expression. For example:

√(2 + √3) = √(2 + 1.732)

In this example, the radical sign (√) is used to express the square root of a compound expression involving another radical expression.

Higher-Order Radical Form

Higher-order radical form is used to express a number as a root of another number, where the order of the root is greater than 2. For example:

³√27 = 3

In this example, the radical sign (√) is used to express the cube root of 27, which is equal to 3.

Properties of Radical Form

Radical form has several properties that make it useful in mathematics:

Distributive Property

The distributive property of radical form states that the radical sign (√) can be distributed over addition and subtraction. For example:

√(a + b) = √a + √b

Associative Property

The associative property of radical form states that the radical sign (√) can be associated with other mathematical operations, such as multiplication and division. For example:

√(ab) = √a√b

Commutative Property

The commutative property of radical form states that the radical sign (√) can be commuted with other mathematical operations, such as addition and subtraction. For example:

√(a + b) = √(b + a)

Applications of Radical Form

Radical form has numerous applications in various fields of mathematics, including:

Algebra

Radical form is used to solve equations involving roots, such as quadratic equations and polynomial equations.

Geometry

Radical form is used to calculate distances and lengths in geometric shapes, such as triangles and circles.

Trigonometry

Radical form is used to solve equations involving trigonometric functions, such as sine and cosine.

Calculus

Radical form is used to solve equations involving limits and derivatives.

Conclusion

In conclusion, radical form is a fundamental concept in mathematics that has numerous applications in various fields. It is used to simplify complex expressions and to solve equations involving roots. The properties of radical form, such as the distributive, associative, and commutative properties, make it a powerful tool in mathematics.

If you have any questions or comments about radical form, please feel free to ask. You can also share this article with others who may be interested in learning about radical form.