What Is 20 In Decimal Form

Quick Links :

Understanding Decimal Forms

The term "20" in mathematics refers to a numerical value that can be expressed in various forms, including decimal. Understanding decimal forms is essential for handling arithmetic operations, converting between different number systems, and representing quantities in various formats.

What is Decimal Form?

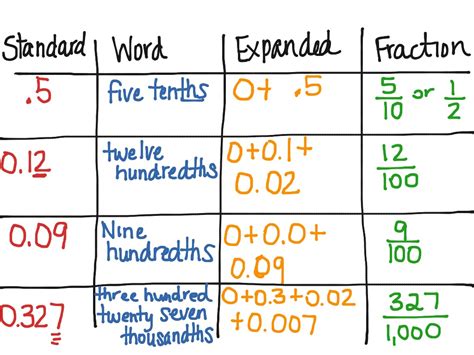
In mathematics, decimal form refers to a way of expressing numbers using the decimal system. This system represents numbers using a point (.) to separate the whole part from the fractional part. The decimal system is a positional notation system that uses powers of 10 to represent numbers.

Converting 20 to Decimal Form

To convert the number 20 to decimal form, we simply write it as 20.0. This is because 20 is a whole number, and in decimal form, whole numbers can be represented with a decimal point and zero fractional digits.

Understanding the Concept of Place Value

In the decimal system, each digit has a place value that depends on its position relative to the decimal point. The place value of a digit is determined by its position, with each position representing a power of 10.

• The first digit to the left of the decimal point has a place value of 10^0 (1).
• The second digit to the left has a place value of 10^1 (10).
• The third digit to the left has a place value of 10^2 (100), and so on.

Similarly, the digits to the right of the decimal point have place values that decrease by powers of 10:

• The first digit to the right has a place value of 10^(-1) (0.1).
• The second digit to the right has a place value of 10^(-2) (0.01), and so on.

In the case of the number 20, it can be broken down as follows:

• 20 = 2 x 10^1 + 0 x 10^0

This representation illustrates the concept of place value and how the decimal system represents numbers.

Importance of Decimal Forms in Mathematics

Decimal forms play a crucial role in various mathematical operations, including:

• Addition and Subtraction: Decimal forms make it easier to perform arithmetic operations, especially when dealing with fractions and decimals.
• Multiplication and Division: Understanding decimal forms helps in performing multiplication and division operations involving decimal numbers.
• Conversion between Number Systems: Decimal forms are essential for converting between different number systems, such as binary, octal, and hexadecimal.
• Real-World Applications: Decimal forms are used extensively in real-world applications, including finance, science, engineering, and data analysis.

Common Applications of Decimal Forms

Decimal forms have numerous practical applications, including:

• Financial Calculations: Decimal forms are used extensively in financial calculations, including interest rates, investments, and currency conversions.
• Scientific Measurements: Decimal forms are used to represent scientific measurements, such as temperatures, weights, and distances.
• Engineering and Architecture: Decimal forms are used in engineering and architecture to represent dimensions, quantities, and measurements.
• Data Analysis: Decimal forms are used in data analysis to represent data, perform statistical calculations, and create visualizations.

Challenges and Limitations of Decimal Forms

While decimal forms are widely used and accepted, there are some challenges and limitations associated with them:

• Rounding Errors: Decimal forms can lead to rounding errors, especially when dealing with irrational numbers or very large/small numbers.
• Precision and Accuracy: Decimal forms can affect the precision and accuracy of calculations, especially when dealing with complex mathematical operations.
• Limited Representation: Decimal forms have limited representation, especially when dealing with very large or very small numbers.

Best Practices for Working with Decimal Forms

To work effectively with decimal forms, follow these best practices:

• Understand the Basics: Understand the basic concepts of decimal forms, including place value, rounding, and significant figures.
• Use Correct Notation: Use correct notation when representing decimal numbers, including the use of decimal points and significant figures.
• Perform Calculations Carefully: Perform calculations carefully, taking into account rounding errors and precision/accuracy considerations.

Conclusion and Future Directions

In conclusion, decimal forms play a vital role in mathematics and have numerous practical applications. However, there are also challenges and limitations associated with decimal forms that need to be addressed.

Future directions for decimal forms include:

• Developing New Notations: Developing new notations and representations that can handle complex mathematical operations and very large/small numbers.
• Improving Precision and Accuracy: Improving precision and accuracy in calculations involving decimal forms.
• Exploring Alternative Number Systems: Exploring alternative number systems, such as binary and hexadecimal, and their applications.

By understanding decimal forms and their importance, we can unlock new possibilities in mathematics, science, and engineering.