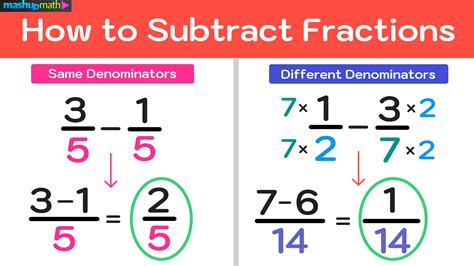
In the world of fractions, understanding equivalent ratios and proportions is crucial. One such ratio is 2 3/2 3, which may seem complex at first, but it's actually quite simple. In this article, we'll break down what 2 3/2 3 means, how it's calculated, and its real-world applications.
What is 2 3/2 3?
To understand 2 3/2 3, let's first break it down into its individual components. The number "2 3" is a mixed number, which is a combination of a whole number (2) and a fraction (3/2). The slash (/) is used to separate the numerator (3) from the denominator (2). So, 2 3/2 3 can be read as "2 and 3/2, over 2 and 3/2".
How to Calculate 2 3/2 3
To calculate 2 3/2 3, we need to follow the order of operations (PEMDAS):
- Multiply the whole number (2) by the denominator (2): 2 × 2 = 4
- Add the numerator (3) to the product: 4 + 3 = 7
- Divide the result by the denominator (2): 7 ÷ 2 = 3.5
So, 2 3/2 3 is equal to 3.5.

Why is 2 3/2 3 Important?
Understanding equivalent ratios like 2 3/2 3 is essential in various real-world applications, such as:
- Cooking: When scaling recipes, equivalent ratios help maintain the balance of ingredients.
- Building: In construction, equivalent ratios ensure that materials are used efficiently and structures are stable.
- Science: Equivalent ratios are used to describe chemical reactions, electrical circuits, and other scientific phenomena.
Simplifying Equivalent Ratios
To simplify equivalent ratios like 2 3/2 3, we can use the following steps:
- Identify the greatest common divisor (GCD) of the numerator and denominator.
- Divide both the numerator and denominator by the GCD.
For example, the GCD of 3 and 2 is 1, so we can't simplify 2 3/2 3 further.
Common Mistakes
When working with equivalent ratios, it's essential to avoid common mistakes, such as:
- Mixed numbers: Failing to convert mixed numbers to improper fractions can lead to errors.
- Fraction simplification: Not simplifying fractions can result in unnecessary complexity.
Real-World Examples
Equivalent ratios are used in various real-world applications, such as:
- Architecture: The Golden Ratio (φ) is an equivalent ratio used in designing aesthetically pleasing buildings.
- Music: Musical intervals and chord progressions rely on equivalent ratios to create harmonious sounds.

Conclusion: Unraveling the Mystery of 2 3/2 3
In conclusion, 2 3/2 3 is a simple yet powerful equivalent ratio that has numerous real-world applications. By understanding how to calculate and simplify equivalent ratios, we can unlock the secrets of proportions and make informed decisions in various fields.
What's Next?
Now that you've grasped the concept of 2 3/2 3, try applying equivalent ratios to real-world problems. Share your experiences and insights in the comments below!
Frequently Asked Questions
What is an equivalent ratio?
+An equivalent ratio is a ratio that has the same value as another ratio, but with different numbers.
How do I simplify an equivalent ratio?
+To simplify an equivalent ratio, divide both the numerator and denominator by their greatest common divisor (GCD).
What are some real-world applications of equivalent ratios?
+Equivalent ratios are used in cooking, building, science, architecture, and music, among other fields.