0.36 As A Fraction In Simplest Form

Quick Links :

The importance of fractions cannot be overstated, as they play a crucial role in various aspects of mathematics, science, and engineering. One common decimal value that is often encountered is 0.36. In this article, we will explore the conversion of 0.36 to a fraction in its simplest form, discuss the underlying mathematical concepts, and provide practical examples and applications.

What is 0.36 as a Fraction?

To convert the decimal 0.36 to a fraction, we need to express it as a ratio of two integers. The resulting fraction is 36/100, which can be simplified further. By dividing both the numerator and denominator by 4, we get:

36 ÷ 4 = 9 100 ÷ 4 = 25

So, the fraction equivalent of 0.36 in simplest form is 9/25.

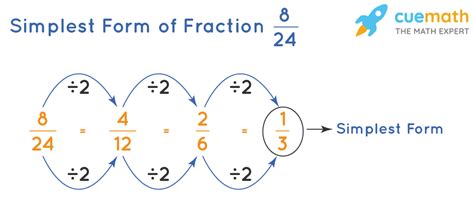
Simplifying Fractions

Simplifying fractions involves reducing them to their lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). This is an essential concept in mathematics, as it helps to:

• Reduce complexity: Simplifying fractions makes them easier to work with, especially when performing calculations or comparisons.
• Avoid confusion: Simplified fractions minimize the risk of errors and misunderstandings, ensuring that calculations are accurate and reliable.
• Improve communication: Simplified fractions facilitate clear and concise communication of mathematical ideas and results.

Working with Fractions

Fractions are an essential part of arithmetic, and working with them requires a solid understanding of the underlying concepts. Here are some key aspects of working with fractions:

• Adding and subtracting fractions: To add or subtract fractions, they must have a common denominator. Once the denominators are the same, the numerators can be added or subtracted.
• Multiplying fractions: To multiply fractions, simply multiply the numerators and denominators separately, then simplify the resulting fraction.
• Dividing fractions: To divide fractions, invert the second fraction (i.e., flip the numerator and denominator) and multiply.

Real-World Applications of Fractions

Fractions have numerous practical applications in various fields, including:

• Cooking and recipes: Fractions are used to measure ingredients and scale recipes up or down.
• Finance and commerce: Fractions are used to calculate interest rates, discounts, and percentages.
• Science and engineering: Fractions are used to represent ratios, proportions, and quantities in fields like physics, chemistry, and mathematics.

Converting Decimals to Fractions

Converting decimals to fractions is a common task in mathematics. Here are some steps to follow:

1. Identify the decimal value to be converted.
2. Determine the place value of the last digit in the decimal.
3. Write the decimal as a fraction with the place value as the denominator.
4. Simplify the fraction, if possible.

Common Decimals and Their Fractional Equivalents

Here are some common decimals and their fractional equivalents:

• 0.5 = 1/2
• 0.25 = 1/4
• 0.75 = 3/4
• 0.1 = 1/10
• 0.01 = 1/100

Conclusion and Next Steps

In this article, we explored the conversion of 0.36 to a fraction in simplest form, discussed the underlying mathematical concepts, and provided practical examples and applications. We hope this information has been helpful in deepening your understanding of fractions and their importance in mathematics.

We invite you to share your thoughts, questions, or examples of how fractions are used in your everyday life. Feel free to comment below, and we'll be happy to engage in a discussion.