Standard Form Of A Circle Homework 9 Unit 10

Quick Links :

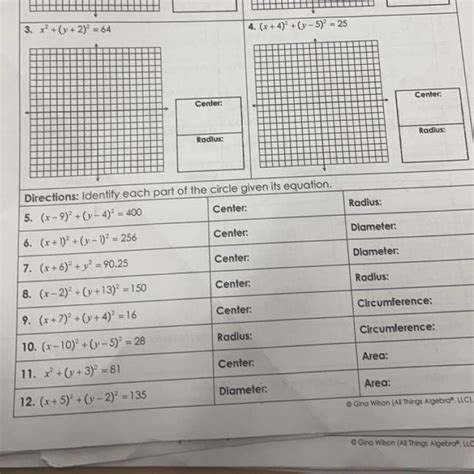
Understanding the standard form of a circle is crucial in mathematics, particularly in geometry and trigonometry. It provides a concise way to describe the properties of a circle, including its center and radius.

What is the Standard Form of a Circle?

The standard form of a circle is an equation that describes a circle in a two-dimensional plane. It is written in the form:

(x - h)^2 + (y - k)^2 = r^2

where (h, k) represents the coordinates of the center of the circle, and r represents the radius of the circle.

Breaking Down the Standard Form

To understand the standard form of a circle, it's essential to break down the components of the equation:

• (x - h) and (y - k) represent the differences between the x and y coordinates of a point on the circle and the center of the circle.
• The squared terms ensure that the equation is always positive, regardless of the signs of (x - h) and (y - k).
• The sum of the squared terms is equal to the square of the radius, which represents the distance between the center and any point on the circle.

How to Graph a Circle in Standard Form

To graph a circle in standard form, follow these steps:

1. Identify the center of the circle by evaluating (h, k).
2. Determine the radius by taking the square root of r^2.
3. Use a compass or a circular object to draw a circle with the center at (h, k) and a radius of r.

Example: Graphing a Circle in Standard Form

Graph the circle with the equation:

(x - 2)^2 + (y - 3)^2 = 16

To graph the circle, follow the steps:

1. Identify the center: (h, k) = (2, 3)
2. Determine the radius: r = √16 = 4
3. Use a compass or a circular object to draw a circle with the center at (2, 3) and a radius of 4.

Advantages of Using the Standard Form

Using the standard form of a circle has several advantages:

• It provides a concise way to describe the properties of a circle.
• It allows for easy identification of the center and radius.
• It enables the calculation of distances and angles within the circle.

Common Applications of the Standard Form

The standard form of a circle is used in various real-world applications, such as:

• Geometry and trigonometry problems
• Circle equations in physics and engineering
• Computer graphics and game development
• Architecture and design

Challenges and Misconceptions

Common challenges and misconceptions when working with the standard form of a circle include:

• Confusing the center and radius with the x and y intercepts.
• Forgetting to square the radius when calculating the equation.
• Incorrectly identifying the center and radius from the equation.

Tips for Overcoming Challenges

To overcome these challenges, follow these tips:

• Double-check the equation and calculations.
• Use visual aids to help identify the center and radius.
• Practice, practice, practice to build confidence and fluency.

Conclusion: Mastering the Standard Form

Mastering the standard form of a circle is essential for success in mathematics and various real-world applications. By understanding the components of the equation, graphing circles, and overcoming common challenges, you can develop a strong foundation in geometry and trigonometry.

We encourage you to share your thoughts and experiences with the standard form of a circle in the comments below. How have you used the standard form in your studies or real-world applications? What challenges have you faced, and how have you overcome them?

FAQ Section: