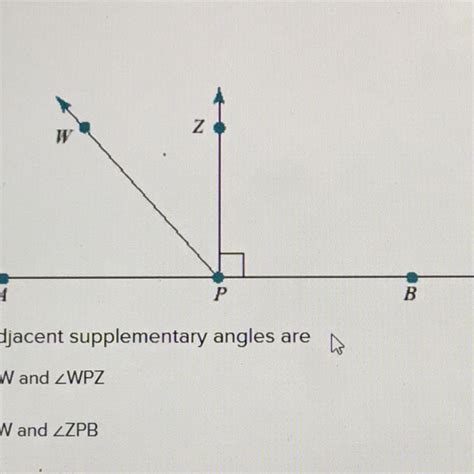
Angles are an essential part of geometry and are used to describe the relationship between two lines or planes that intersect. There are several types of angles, including acute, right, obtuse, and straight angles. In this article, we will focus on supplementary angles and how two adjacent supplementary angles form a straight line.
Understanding Angles

Angles are formed when two lines or planes intersect. The point where the lines or planes intersect is called the vertex. Angles can be classified into different types based on their measure. Acute angles are those that measure less than 90 degrees, right angles are those that measure exactly 90 degrees, obtuse angles are those that measure greater than 90 degrees, and straight angles are those that measure exactly 180 degrees.
Supplementary Angles

Supplementary angles are two angles whose measures add up to 180 degrees. In other words, if you have two angles and their sum is 180 degrees, then they are supplementary angles. For example, if you have an angle of 60 degrees and another angle of 120 degrees, then they are supplementary angles because their sum is 180 degrees.
Adjacent Supplementary Angles

Adjacent supplementary angles are two supplementary angles that share a common vertex and lie on the same side of the line or plane. When two adjacent supplementary angles are formed, they create a straight line. This is because the sum of their measures is 180 degrees, which is the same as the measure of a straight line.
Why Two Adjacent Supplementary Angles Form a Straight Line

Two adjacent supplementary angles form a straight line because their sum is 180 degrees. When two angles are supplementary, it means that they complete each other to form a straight line. Think of it like a puzzle piece - when two supplementary angles are put together, they form a complete picture, which is a straight line.
Example
Let's consider an example to illustrate this concept. Suppose we have two adjacent supplementary angles, angle A and angle B. Angle A measures 70 degrees, and angle B measures 110 degrees. Since their sum is 180 degrees (70 + 110 = 180), they are supplementary angles. When we put them together, they form a straight line.
Benefits of Understanding Supplementary Angles

Understanding supplementary angles has several benefits. It helps us to solve problems involving angles and to visualize how different angles relate to each other. Additionally, it is essential in various fields such as architecture, engineering, and design, where precise calculations of angles are crucial.
Real-World Applications
Supplementary angles have numerous real-world applications. For instance, in architecture, supplementary angles are used to design buildings and bridges. In engineering, they are used to calculate the stress and strain on materials. In design, they are used to create visually appealing and balanced compositions.
Conclusion and Future Directions
In conclusion, two adjacent supplementary angles form a straight line because their sum is 180 degrees. Understanding supplementary angles is crucial in various fields and has numerous real-world applications. As we continue to explore and apply the concept of supplementary angles, we can expect to see new innovations and breakthroughs in fields such as architecture, engineering, and design.
What are your thoughts on supplementary angles? Share your comments and insights below.
What is the sum of two supplementary angles?
+The sum of two supplementary angles is 180 degrees.
What is the difference between adjacent and non-adjacent supplementary angles?
+Adjacent supplementary angles share a common vertex and lie on the same side of the line or plane, whereas non-adjacent supplementary angles do not share a common vertex and may lie on different sides of the line or plane.
Can two supplementary angles be acute angles?
+No, two supplementary angles cannot be acute angles because their sum would be less than 180 degrees.