Understanding the concept of vectors is crucial in mathematics and physics, as it helps describe quantities with both magnitude and direction. One of the key aspects of vectors is representing them in different forms, and the trigonometric form is one of the most useful and widely used methods. In this article, we will delve into the world of vectors and explore the trigonometric form in detail, providing a comprehensive explanation of its benefits, working mechanisms, and applications.
What is a Vector?

A vector is a mathematical object that has both magnitude (length) and direction. It is often represented graphically as an arrow in a coordinate system, with the length of the arrow representing the magnitude and the direction of the arrow representing the direction of the vector. Vectors can be used to represent various physical quantities such as displacement, velocity, acceleration, and force.
Why is the Trigonometric Form Important?

The trigonometric form of a vector is essential in mathematics and physics because it provides a convenient and powerful way to represent and manipulate vectors. This form allows us to express vectors in terms of their magnitude and direction, making it easier to perform calculations and operations involving vectors. The trigonometric form is particularly useful in applications such as:
- Calculating distances and angles between vectors
- Finding the magnitude and direction of resultant vectors
- Resolving vectors into their component parts
- Describing the motion of objects in terms of their position, velocity, and acceleration
How to Represent a Vector in Trigonometric Form
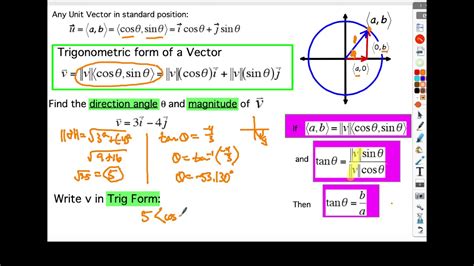
To represent a vector in trigonometric form, we need to specify its magnitude (length) and direction. The direction of the vector is typically represented using angles, and the trigonometric form uses the sine and cosine functions to relate the vector's components to its magnitude and direction.The trigonometric form of a vector can be written as:
r = (x, y) = (r cos θ, r sin θ)
where:
- r is the magnitude (length) of the vector
- θ is the angle between the vector and the x-axis
- x and y are the components of the vector along the x and y axes, respectively
Benefits of the Trigonometric Form

The trigonometric form of a vector offers several benefits, including:
- Simplifies calculations: The trigonometric form makes it easier to perform calculations involving vectors, such as finding the magnitude and direction of resultant vectors.
- Provides a unified framework: The trigonometric form provides a unified framework for representing and manipulating vectors, making it easier to work with vectors in different contexts.
- Facilitates geometric interpretations: The trigonometric form allows for geometric interpretations of vector operations, making it easier to visualize and understand the results of calculations.
Applications of the Trigonometric Form
The trigonometric form has numerous applications in mathematics, physics, engineering, and other fields. Some examples include:- Navigation and surveying: The trigonometric form is used in navigation and surveying to calculate distances and angles between locations.
- Physics and engineering: The trigonometric form is used to describe the motion of objects in terms of their position, velocity, and acceleration.
- Computer graphics: The trigonometric form is used in computer graphics to perform transformations and projections on vectors.
Steps to Convert a Vector to Trigonometric Form

Converting a vector to trigonometric form involves the following steps:
- Find the magnitude: Calculate the magnitude (length) of the vector using the formula: r = √(x^2 + y^2)
- Find the angle: Calculate the angle θ between the vector and the x-axis using the formula: θ = arctan(y/x)
- Write the vector in trigonometric form: Write the vector in trigonometric form using the formula: r = (r cos θ, r sin θ)
Common Mistakes to Avoid

When working with the trigonometric form of a vector, there are several common mistakes to avoid, including:
- Incorrectly calculating the angle: Make sure to calculate the angle θ correctly using the arctan function.
- Forgetting to include the magnitude: Make sure to include the magnitude r when writing the vector in trigonometric form.
- Mixing up the sine and cosine functions: Make sure to use the correct trigonometric function (sine or cosine) when writing the vector in trigonometric form.
Conclusion
In conclusion, the trigonometric form of a vector is a powerful and essential tool in mathematics and physics. By representing vectors in terms of their magnitude and direction, the trigonometric form provides a convenient and unified framework for performing calculations and operations involving vectors. By following the steps outlined in this article, you can easily convert vectors to trigonometric form and avoid common mistakes.Share Your Thoughts
Do you have any experience working with vectors in trigonometric form? Share your thoughts and insights in the comments below. If you have any questions or need further clarification, feel free to ask.What is the main advantage of the trigonometric form of a vector?
+The main advantage of the trigonometric form of a vector is that it provides a convenient and unified framework for representing and manipulating vectors.
How do I calculate the angle θ between a vector and the x-axis?
+You can calculate the angle θ between a vector and the x-axis using the formula: θ = arctan(y/x)
What is the difference between the sine and cosine functions in the trigonometric form of a vector?
+The sine function is used to represent the y-component of the vector, while the cosine function is used to represent the x-component.