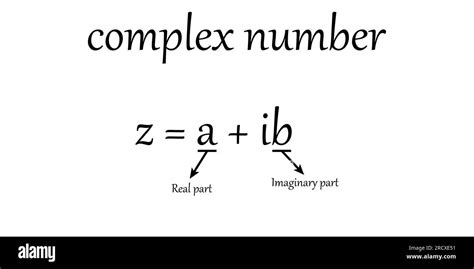Complex Numbers In Standard Form Explained Simply

Quick Links :

Hide

Complex numbers have been a cornerstone of mathematics and physics for centuries, allowing us to solve equations and represent quantities that cannot be expressed using real numbers alone. However, for many students, the concept of complex numbers can be intimidating, especially when it comes to standard form. In this article, we will break down the concept of complex numbers in standard form, explaining it in simple terms, and providing practical examples to help solidify your understanding.

What Are Complex Numbers?

Complex numbers are a combination of real and imaginary numbers. A real number is a number that can be found on the number line, such as 1, 2, or 3. An imaginary number, on the other hand, is a number that, when squared, gives a negative result. The most common imaginary number is the square root of -1, denoted by i.

Standard Form of Complex Numbers

A complex number can be written in standard form as:

a + bi

where a is the real part, b is the imaginary part, and i is the imaginary unit (i.e., the square root of -1).

For example, the complex number 3 + 4i has a real part of 3 and an imaginary part of 4.

How to Write Complex Numbers in Standard Form

To write a complex number in standard form, you need to identify the real and imaginary parts. Here are the steps:

1. Identify the real part: The real part is the part of the complex number that is not multiplied by i.
2. Identify the imaginary part: The imaginary part is the part of the complex number that is multiplied by i.
3. Write the complex number in the form a + bi, where a is the real part and b is the imaginary part.

Examples of Complex Numbers in Standard Form

Here are a few examples of complex numbers in standard form:

• 2 + 3i (real part: 2, imaginary part: 3)
• 5 - 2i (real part: 5, imaginary part: -2)
• 0 + 4i (real part: 0, imaginary part: 4)

Operations with Complex Numbers in Standard Form

Complex numbers in standard form can be added, subtracted, multiplied, and divided using the following rules:

• Addition: (a + bi) + (c + di) = (a + c) + (b + d)i
• Subtraction: (a + bi) - (c + di) = (a - c) + (b - d)i
• Multiplication: (a + bi)(c + di) = (ac - bd) + (ad + bc)i
• Division: (a + bi) / (c + di) = ((ac + bd) / (c^2 + d^2)) + ((bc - ad) / (c^2 + d^2))i

Examples of Operations with Complex Numbers

Here are a few examples of operations with complex numbers in standard form:

• (2 + 3i) + (1 + 2i) = (2 + 1) + (3 + 2)i = 3 + 5i
• (5 - 2i) - (3 - 1i) = (5 - 3) + (-2 + 1)i = 2 - i
• (2 + 3i)(1 + 2i) = (2 - 6) + (4 + 3)i = -4 + 7i

Applications of Complex Numbers in Standard Form

Complex numbers in standard form have many applications in mathematics, physics, and engineering. Some examples include:

• Solving quadratic equations that cannot be factored
• Representing quantities that cannot be expressed using real numbers alone, such as electrical impedance and voltage
• Analyzing signals and filters in electronics and communication systems
• Modeling population growth and predator-prey relationships in biology

Real-World Examples of Complex Numbers

Here are a few real-world examples of complex numbers in standard form:

• Electrical engineers use complex numbers to analyze and design electronic circuits.
• Signal processing engineers use complex numbers to analyze and filter signals in communication systems.
• Biologists use complex numbers to model population growth and predator-prey relationships.

We hope this article has helped you understand complex numbers in standard form. Complex numbers are a powerful tool for solving equations and representing quantities that cannot be expressed using real numbers alone. By following the steps outlined in this article, you can write complex numbers in standard form and perform operations with them. Remember to practice, practice, practice!

Now, it's your turn! Do you have any questions about complex numbers in standard form? Share them with us in the comments below. Don't forget to like and share this article with your friends and classmates who may be struggling with complex numbers.