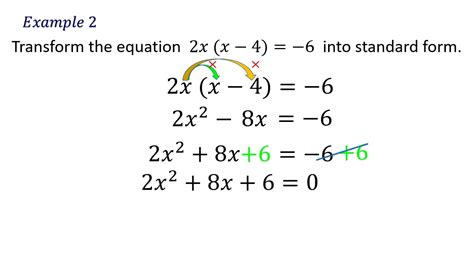Master The Standard Form Of A Quadratic Equation Easily

Quick Links :

The quadratic equation - a fundamental concept in algebra that has been a cornerstone of mathematics for centuries. It's a formula that has been used to solve countless problems, from the simplest equations to the most complex ones. But have you ever wondered what the standard form of a quadratic equation is? In this article, we'll delve into the world of quadratic equations, explore the standard form, and provide you with a comprehensive guide on how to master it easily.

What is a Quadratic Equation?

A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. It's an equation that can be written in the form of ax^2 + bx + c = 0, where a, b, and c are constants, and x is the variable. Quadratic equations can be used to model a wide range of real-world phenomena, such as the trajectory of a projectile, the growth of a population, or the vibration of a spring.

What is the Standard Form of a Quadratic Equation?

The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants, and a cannot be equal to zero. This is the most common form of a quadratic equation, and it's the one that you'll encounter most often in mathematics and science. The standard form is useful because it allows us to easily identify the coefficients of the equation, which is essential for solving it.

How to Identify the Standard Form of a Quadratic Equation

Identifying the standard form of a quadratic equation is relatively straightforward. Here are the steps to follow:

• Check if the equation is a polynomial of degree two. If it is, then it's a quadratic equation.
• Check if the equation is in the form of ax^2 + bx + c = 0. If it is, then it's in standard form.
• Identify the coefficients a, b, and c. Make sure that a is not equal to zero.

Examples of Quadratic Equations in Standard Form

• x^2 + 4x + 4 = 0
• 2x^2 - 3x - 1 = 0
• x^2 - 2x - 6 = 0

How to Solve Quadratic Equations in Standard Form

Solving quadratic equations in standard form is a bit more involved, but it's still a manageable task. Here are the steps to follow:

• Factor the equation, if possible. This involves finding two binomials whose product is equal to the original equation.
• Use the quadratic formula, if the equation cannot be factored. The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a.
• Check the solutions to make sure they are valid.

Examples of Solving Quadratic Equations in Standard Form

• x^2 + 4x + 4 = 0 can be factored as (x + 2)(x + 2) = 0, which has a solution of x = -2.
• 2x^2 - 3x - 1 = 0 cannot be factored, so we use the quadratic formula to get x = (3 ± √(9 - 4(2)(-1))) / 4 = (3 ± √25) / 4 = (3 ± 5) / 4.

Conclusion: Mastering the Standard Form of a Quadratic Equation

Mastering the standard form of a quadratic equation is an essential skill in mathematics and science. With practice and patience, you can become proficient in identifying and solving quadratic equations in standard form. Remember to always check if the equation is in the correct form, identify the coefficients, and use the quadratic formula if necessary. By following these steps, you'll be well on your way to mastering the standard form of a quadratic equation.

We hope this article has been informative and helpful in your journey to master the standard form of a quadratic equation. If you have any questions or comments, please feel free to share them below. Don't forget to share this article with your friends and colleagues who may also benefit from it.