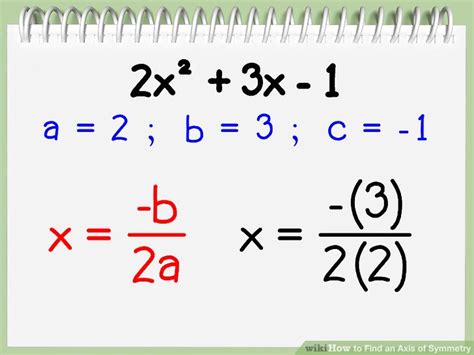5 Ways To Find Axis Of Symmetry In Standard Form

Quick Links :

Finding the axis of symmetry in a standard form quadratic equation can be a challenge, but with the right strategies, it can be made easier. In this article, we will explore five different ways to find the axis of symmetry in a standard form quadratic equation, along with practical examples and explanations.

Understanding the Axis of Symmetry

The axis of symmetry is a line that divides a quadratic equation's graph into two symmetrical parts. It is a vertical line that passes through the vertex of the parabola, which is the minimum or maximum point of the graph. In a standard form quadratic equation, the axis of symmetry can be found using various methods.

Method 1: Using the Formula

One of the simplest ways to find the axis of symmetry is by using the formula x = -b / 2a, where a, b, and c are the coefficients of the quadratic equation in standard form (ax^2 + bx + c = 0).

For example, find the axis of symmetry of the quadratic equation x^2 + 4x + 4 = 0.

Using the formula, x = -b / 2a = -4 / (2*1) = -2.

Therefore, the axis of symmetry is x = -2.

Method 2: Completing the Square

Another method to find the axis of symmetry is by completing the square. This method involves rewriting the quadratic equation in vertex form (a(x - h)^2 + k = 0), where (h, k) is the vertex of the parabola.

For example, find the axis of symmetry of the quadratic equation x^2 + 6x + 8 = 0.

Complete the square by adding and subtracting (b/2)^2 = (6/2)^2 = 9 to the equation:

x^2 + 6x + 9 - 9 + 8 = 0

(x + 3)^2 - 1 = 0

(x + 3)^2 = 1

x + 3 = ±√1

x = -3 ± 1

x = -2 or x = -4

Since the axis of symmetry passes through the vertex, which is (-3, -1), the axis of symmetry is x = -3.

Method 3: Using the Graph

If you have a graph of the quadratic equation, you can find the axis of symmetry by identifying the vertical line that passes through the vertex.

For example, find the axis of symmetry of the quadratic equation x^2 - 4x - 3 = 0.

By graphing the equation, we can see that the vertex is at (-1, -4). Therefore, the axis of symmetry is x = -1.

Method 4: Using the Factored Form

If the quadratic equation is in factored form (a(x - p)(x - q) = 0), you can find the axis of symmetry by finding the midpoint of the roots.

For example, find the axis of symmetry of the quadratic equation (x - 2)(x + 2) = 0.

The roots of the equation are x = 2 and x = -2. The midpoint of the roots is x = (2 + (-2))/2 = 0.

Therefore, the axis of symmetry is x = 0.

Method 5: Using the Vertex Form

If the quadratic equation is in vertex form (a(x - h)^2 + k = 0), you can find the axis of symmetry by identifying the value of h.

For example, find the axis of symmetry of the quadratic equation (x - 2)^2 + 1 = 0.

The vertex is at (2, 1), so the axis of symmetry is x = 2.

In conclusion, finding the axis of symmetry in a standard form quadratic equation can be achieved using various methods, including using the formula, completing the square, using the graph, using the factored form, and using the vertex form. By understanding and applying these methods, you can easily find the axis of symmetry in any quadratic equation.

We hope you found this article informative and helpful. If you have any questions or need further clarification, please leave a comment below. Don't forget to share this article with your friends and classmates who may benefit from it.