Simplify Square Root Of 98 In 3 Easy Steps

Simplifying square roots can be a challenging task, especially for students who are new to mathematics. However, with a step-by-step approach, simplifying square roots can become a breeze. In this article, we will simplify the square root of 98 in 3 easy steps.
The square root of 98 is a number that, when multiplied by itself, gives the result 98. To simplify this, we need to find the largest perfect square that divides 98. A perfect square is a number that can be expressed as the product of an integer with itself. For example, 16 is a perfect square because it can be expressed as 4 × 4.
Step 1: Find the Prime Factorization of 98
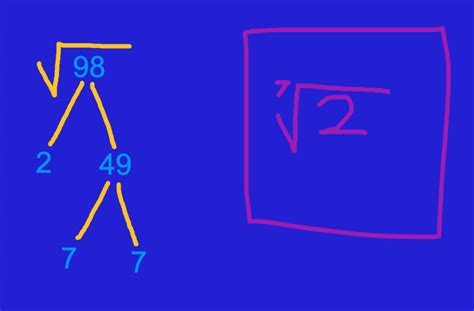
The first step to simplify the square root of 98 is to find its prime factorization. Prime factorization is the process of breaking down a number into its prime factors. The prime factors of 98 are 2, 7, and 7.To find the prime factorization of 98, we can start by dividing it by the smallest prime number, which is 2. Since 98 is an even number, it can be divided by 2.
98 ÷ 2 = 49
Next, we need to find the prime factors of 49. The prime factors of 49 are 7 and 7.
49 = 7 × 7
Therefore, the prime factorization of 98 is:
98 = 2 × 7 × 7
Step 2: Identify the Perfect Square Factor

Now that we have the prime factorization of 98, we need to identify the perfect square factor. A perfect square factor is a factor that can be expressed as the product of an integer with itself.
In the prime factorization of 98, we have two 7s, which means we have a perfect square factor of 7 × 7 = 49.
Step 3: Simplify the Square Root
The final step is to simplify the square root of 98. To do this, we can rewrite the square root of 98 as the product of the perfect square factor and the remaining factor.√98 = √(2 × 7 × 7) = √(2) × √(7 × 7) = √2 × √49 = √2 × 7
Therefore, the simplified square root of 98 is √2 × 7.
Benefits of Simplifying Square Roots

Simplifying square roots has several benefits, including:
- Easier calculations: Simplifying square roots can make calculations easier and faster.
- Improved understanding: Simplifying square roots can help students understand the underlying mathematical concepts.
- Better problem-solving skills: Simplifying square roots can help students develop better problem-solving skills.
Real-World Applications of Square Roots

Square roots have several real-world applications, including:
- Architecture: Square roots are used in architecture to design buildings and bridges.
- Engineering: Square roots are used in engineering to calculate the stress and strain on materials.
- Computer science: Square roots are used in computer science to develop algorithms and models.
Conclusion
Simplifying square roots can be a challenging task, but with a step-by-step approach, it can become easier. By following the three easy steps outlined in this article, students can simplify the square root of 98 and develop a better understanding of mathematical concepts.What is the simplified square root of 98?
+The simplified square root of 98 is √2 × 7.
What are the benefits of simplifying square roots?
+The benefits of simplifying square roots include easier calculations, improved understanding, and better problem-solving skills.
What are the real-world applications of square roots?
+Square roots have several real-world applications, including architecture, engineering, and computer science.
We hope this article has been helpful in simplifying the square root of 98. If you have any further questions or would like to share your thoughts, please leave a comment below.