Square Root Of 61 In Radical Form Simplified

Quick Links :

The square root of 61 is a fascinating mathematical concept that has intrigued mathematicians and students alike for centuries. In this article, we will delve into the world of radicals and explore the square root of 61 in its simplified form.

What is the Square Root of 61?

The square root of 61 is a number that, when multiplied by itself, gives the result of 61. This mathematical operation is denoted by the symbol √61. In other words, √61 is a value that satisfies the equation:

√61 × √61 = 61

Why is the Square Root of 61 Important?

The square root of 61 has numerous applications in various fields, including mathematics, physics, engineering, and computer science. For instance, it is used in calculations involving right triangles, circles, and waves. Additionally, the square root of 61 is a fundamental concept in algebra and geometry, helping to solve equations and theorems.

The Simplified Radical Form of √61

To simplify the radical form of √61, we need to express it in terms of the product of a rational number and a square root. This can be achieved by factoring the number 61.

61 = 1 × 61

Since 61 is a prime number, it cannot be factored further. Therefore, the simplified radical form of √61 is simply √61.

Properties of the Square Root of 61

Here are some interesting properties of the square root of 61:

• The square root of 61 is an irrational number, meaning it cannot be expressed as a finite decimal or fraction.
• The square root of 61 is a real number, as it lies on the real number line.
• The square root of 61 is a positive number, since the square of any real number is always non-negative.

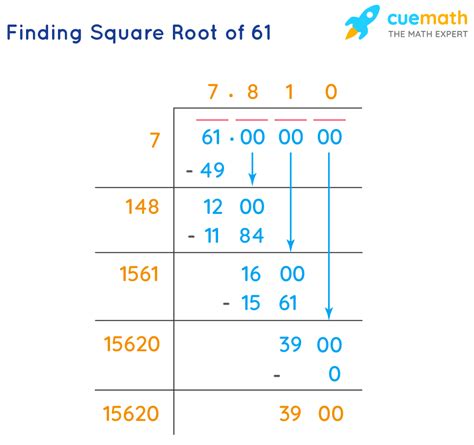
Calculating the Square Root of 61

There are several methods to calculate the square root of 61, including:

• Using a calculator or computer software
• Employing numerical methods, such as the Babylonian method or the Newton-Raphson method
• Utilizing algebraic techniques, such as the quadratic formula

Here is an example of how to calculate the square root of 61 using the Babylonian method:

1. Start with an initial estimate of the square root, such as 8.
2. Divide 61 by the estimate, giving 61 ÷ 8 = 7.625.
3. Take the average of the estimate and the result, giving (8 + 7.625) ÷ 2 = 7.8125.
4. Repeat steps 2-3 until the desired level of precision is achieved.

Applications of the Square Root of 61

The square root of 61 has numerous practical applications in various fields, including:

• Construction: The square root of 61 is used in calculations involving right triangles and building design.
• Physics: The square root of 61 is used in calculations involving waves and vibrations.
• Computer Science: The square root of 61 is used in algorithms and data analysis.

Conclusion: The Square Root of 61

In conclusion, the square root of 61 is an important mathematical concept with numerous applications in various fields. Its simplified radical form is simply √61, and it has several interesting properties, including being an irrational and real number. Calculating the square root of 61 can be achieved using various methods, including numerical and algebraic techniques.

We invite you to share your thoughts and experiences with the square root of 61 in the comments section below. Have you encountered this mathematical concept in your studies or work? How do you think it can be applied in real-world scenarios?