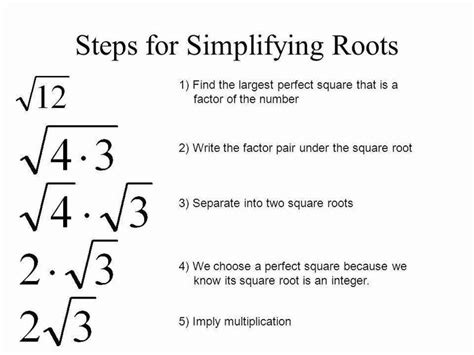
Simplifying Square Root Of 50 To Simplest Radical Form

Quick Links :

Simplifying square roots to their simplest radical form is an essential skill in mathematics, particularly in algebra and geometry. The square root of 50 is a common problem that requires simplification to make it easier to work with. In this article, we will explore the steps to simplify the square root of 50 to its simplest radical form.

The importance of simplifying square roots cannot be overstated. Simplifying square roots makes it easier to perform mathematical operations, such as multiplication and division, and to compare the size of different quantities. In addition, simplifying square roots is a crucial step in solving many mathematical problems, including quadratic equations and trigonometry problems.

So, how do we simplify the square root of 50? The first step is to identify the largest perfect square that divides 50. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. For example, 4, 9, and 16 are perfect squares because they can be expressed as 2^2, 3^2, and 4^2, respectively.

The largest perfect square that divides 50 is 25, which is equal to 5^2. We can rewrite 50 as 25 x 2, where 25 is a perfect square.

Breaking Down the Square Root of 50

To simplify the square root of 50, we can break it down as follows:

√50 = √(25 x 2)

Using the property of square roots that √(ab) = √a x √b, we can rewrite the expression as:

√50 = √25 x √2

Since √25 is equal to 5, we can simplify the expression further:

√50 = 5√2

Therefore, the simplified radical form of the square root of 50 is 5√2.

Why is it Important to Simplify Square Roots?

Simplifying square roots is important for several reasons:

• It makes mathematical operations easier to perform.
• It helps to compare the size of different quantities.
• It is a crucial step in solving many mathematical problems.
• It helps to identify patterns and relationships between numbers.

In addition, simplifying square roots is a fundamental concept in mathematics that is used in many real-world applications, such as physics, engineering, and finance.

Real-World Applications of Simplifying Square Roots

Simplifying square roots has many real-world applications. For example:

• In physics, simplifying square roots is used to calculate the length of the hypotenuse of a right triangle.
• In engineering, simplifying square roots is used to calculate the area of a triangle.
• In finance, simplifying square roots is used to calculate the interest rate on a loan.

In conclusion, simplifying the square root of 50 to its simplest radical form is an essential skill in mathematics. By identifying the largest perfect square that divides 50 and using the property of square roots, we can simplify the expression to 5√2. Simplifying square roots is important for many reasons, including making mathematical operations easier to perform, helping to compare the size of different quantities, and being a crucial step in solving many mathematical problems.

We hope this article has been informative and helpful in explaining the concept of simplifying square roots. If you have any questions or comments, please feel free to share them below.