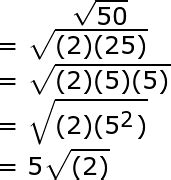Square Root Of 50 In Radical Form Explained

Quick Links :

Square Root of 50 in Radical Form Explained

The square root of 50 is a mathematical expression that represents a value that, when multiplied by itself, gives 50. In this article, we will explore the concept of square roots, radical form, and how to simplify the square root of 50.

What is a Square Root?

A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. The square root symbol is denoted by √. In this case, the square root of 50 can be expressed as √50.

What is Radical Form?

Radical form, also known as simplest radical form, is a way of expressing a square root in a simplified form. It involves factoring the number under the square root sign into a product of prime numbers. The goal is to find the largest perfect square that divides the number, leaving a smaller number under the square root sign.

Simplifying the Square Root of 50

To simplify the square root of 50, we need to find the largest perfect square that divides 50. The factors of 50 are 1, 2, 5, 10, 25, and 50. Among these factors, 25 is the largest perfect square that divides 50.

Step-by-Step Simplification of √50

Here's the step-by-step simplification of √50:

1. Factor 50 into a product of prime numbers: 50 = 2 × 5 × 5
2. Identify the largest perfect square that divides 50: 25 = 5 × 5
3. Write the square root of 50 as a product of the square root of 25 and the square root of the remaining factor: √50 = √(25 × 2)
4. Simplify the expression: √50 = 5√2

Why is the Square Root of 50 Important?

The square root of 50 is important in various mathematical and scientific applications, such as:

• Algebra: Square roots are used to solve quadratic equations and inequalities.
• Geometry: Square roots are used to find the length of the hypotenuse of a right triangle.
• Physics: Square roots are used to calculate distances, velocities, and accelerations.
• Engineering: Square roots are used to design and optimize systems, such as bridges and buildings.

Real-World Applications of √50

The square root of 50 has many real-world applications, including:

• Calculating the length of a shadow: If the height of an object is 50 meters, and the angle of elevation is 30°, the length of the shadow can be calculated using the square root of 50.
• Designing a roller coaster: The square root of 50 can be used to calculate the height of a roller coaster hill, given the velocity and acceleration of the coaster.
• Optimizing a solar panel array: The square root of 50 can be used to calculate the optimal angle of a solar panel array, given the latitude and longitude of the location.

Conclusion

In conclusion, the square root of 50 in radical form is an important mathematical concept with many real-world applications. By simplifying the square root of 50 to 5√2, we can use it to solve problems in algebra, geometry, physics, and engineering.

If you have any questions or comments about the square root of 50, please leave them below. Share this article with your friends and colleagues who may find it useful.