Square Root Of 5 In Radical Form Simplified

Quick Links :

The concept of square roots and radicals is a fundamental aspect of mathematics, particularly in algebra and geometry. In this article, we will delve into the world of radicals, exploring the square root of 5 in its simplified radical form. But before we dive into the specifics, let's take a step back and understand the significance of radicals in mathematics.

Radicals play a crucial role in mathematics, as they allow us to solve equations that cannot be expressed using rational numbers. The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 16 is 4, because 4 multiplied by 4 equals 16. However, not all numbers have a perfect square root. This is where radicals come into play.

A radical is a symbol that represents the nth root of a number. The most common radical is the square root, which is denoted by the symbol √. Radicals can be simplified or expressed in a more complex form, depending on the context. In this article, we will focus on the square root of 5 in its simplified radical form.

What is the Square Root of 5?

The square root of 5 is a value that, when multiplied by itself, gives the number 5. However, 5 does not have a perfect square root, which means it cannot be expressed as a simple integer. Instead, it can be expressed as a decimal or in radical form.

Decimal Representation

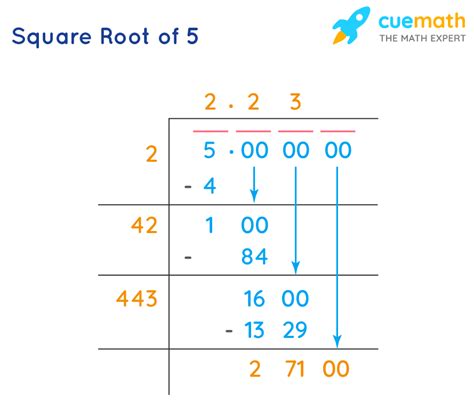
The decimal representation of the square root of 5 is approximately 2.236067977. This value is an approximation, as the actual value of the square root of 5 is an irrational number.

Radical Representation

The radical representation of the square root of 5 is √5. This is the simplest form of the square root of 5, and it is often used in mathematical equations and formulas.

Simplifying the Square Root of 5

The square root of 5 can be simplified further by expressing it as a product of square roots. This can be achieved by using the prime factorization of 5, which is simply 5.

√5 = √(5 × 1) = √5 × √1 = √5

As you can see, the square root of 5 cannot be simplified further. It is already in its simplest radical form.

Working with the Square Root of 5

When working with the square root of 5, it is essential to follow the rules of radicals. Here are some examples:

• Multiplying radicals: √5 × √5 = 5
• Dividing radicals: √5 ÷ √5 = 1
• Adding radicals: √5 + √5 = 2√5
• Subtracting radicals: √5 - √5 = 0

Using the Square Root of 5 in Equations

The square root of 5 can be used in various mathematical equations, such as algebraic equations and geometric formulas. Here are some examples:

• Algebraic equation: x^2 = 5
• Geometric formula: Area of a square = side^2 = (√5)^2 = 5

Applications of the Square Root of 5

The square root of 5 has numerous applications in various fields, including mathematics, physics, engineering, and computer science. Here are some examples:

• Mathematics: The square root of 5 is used in algebra, geometry, and calculus.
• Physics: The square root of 5 is used in the calculation of distances, velocities, and energies.
• Engineering: The square root of 5 is used in the design of bridges, buildings, and electronic circuits.
• Computer Science: The square root of 5 is used in algorithms and data structures.

Conclusion

In conclusion, the square root of 5 is a fundamental concept in mathematics that has numerous applications in various fields. Its simplified radical form is √5, which is an irrational number that cannot be expressed as a simple integer. By understanding the properties and applications of the square root of 5, we can gain a deeper appreciation for the beauty and complexity of mathematics.

If you have any questions or comments about the square root of 5, please feel free to share them below.