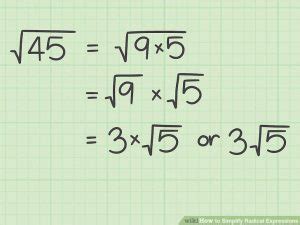Simplifying Roots: Square Root Of 45 In Radical Form

Quick Links :

Simplifying roots can be a challenging task, especially when dealing with numbers that are not perfect squares. The square root of 45 is one such example, and understanding how to simplify it can be a valuable skill in mathematics.

The square root of 45 can be simplified using the concept of radical expressions. Radical expressions are mathematical expressions that contain a square root symbol (√) and are used to represent numbers that cannot be expressed as simple fractions. To simplify the square root of 45, we need to look for perfect squares that divide into 45.

Understanding Radical Expressions

Radical expressions are used to represent numbers that cannot be expressed as simple fractions. They consist of a radical symbol (√) and a radicand, which is the number inside the radical symbol. Radical expressions can be simplified by factoring out perfect squares from the radicand.

Perfect Squares and Radical Expressions

Perfect squares are numbers that can be expressed as the square of an integer. For example, 4, 9, and 16 are perfect squares because they can be expressed as the square of 2, 3, and 4, respectively. Radical expressions can be simplified by factoring out perfect squares from the radicand.

Simplifying the Square Root of 45

To simplify the square root of 45, we need to look for perfect squares that divide into 45. We can start by factoring 45 into its prime factors: 45 = 3 × 3 × 5. We can then look for perfect squares that divide into 45 by grouping the prime factors in pairs.

Factoring 45 into Perfect Squares

We can factor 45 into perfect squares by grouping the prime factors in pairs. One way to do this is to group the two 3's together: 45 = 9 × 5. We can then take the square root of 9, which is 3, and write the simplified radical expression as: √45 = √(9 × 5) = 3√5.

Benefits of Simplifying Radical Expressions

Simplifying radical expressions can have several benefits. One benefit is that it can make calculations easier by reducing the complexity of the expression. Simplifying radical expressions can also make it easier to compare and add expressions.

Real-World Applications of Simplifying Radical Expressions

Simplifying radical expressions has several real-world applications. One example is in physics, where radical expressions are used to describe the motion of objects. By simplifying radical expressions, physicists can make calculations easier and more accurate.

Step-by-Step Guide to Simplifying Radical Expressions

Here is a step-by-step guide to simplifying radical expressions:

1. Factor the radicand into its prime factors.
2. Group the prime factors in pairs.
3. Take the square root of each pair.
4. Write the simplified radical expression.

Common Mistakes to Avoid When Simplifying Radical Expressions

There are several common mistakes to avoid when simplifying radical expressions. One mistake is to forget to factor the radicand into its prime factors. Another mistake is to group the prime factors incorrectly.

Conclusion

Simplifying the square root of 45 can be a challenging task, but by using the concept of radical expressions and factoring out perfect squares, we can simplify the expression to 3√5. By understanding the benefits and applications of simplifying radical expressions, we can make calculations easier and more accurate.

We encourage you to share your thoughts and questions in the comments section below. Have you ever struggled with simplifying radical expressions? What methods do you use to simplify them? Share your experiences and tips with us!