Simplify Radicals: Square Root Of 33

Quick Links :

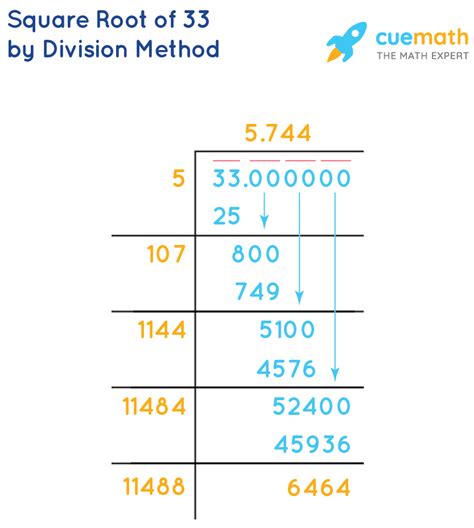
Simplifying radicals is an essential math concept that helps us break down complex expressions into more manageable parts. In this article, we'll focus on simplifying the square root of 33, and explore the steps and techniques involved.

Understanding Square Roots

Before we dive into simplifying the square root of 33, let's quickly review what square roots are. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16.

What is the Square Root of 33?

The square root of 33 is a radical expression that represents the value that, when multiplied by itself, gives 33. However, 33 is not a perfect square, meaning it cannot be expressed as a product of an integer multiplied by itself. Therefore, we need to simplify the radical expression.

How to Simplify Radicals

To simplify radicals, we look for perfect squares that can be factored out of the radicand (the number inside the square root). Here are the steps to simplify radicals:

1. Find perfect squares: Look for perfect squares that divide the radicand.
2. Factor out perfect squares: Write the radicand as a product of the perfect square and another number.
3. Simplify the radical: Take the square root of the perfect square and multiply it by the remaining number.

Simplifying the Square Root of 33

Let's apply these steps to simplify the square root of 33:

1. Find perfect squares: The perfect squares that divide 33 are 1 and 9.
2. Factor out perfect squares: We can write 33 as 9 × 3 + 6.
3. Simplify the radical: Take the square root of 9, which is 3, and multiply it by the remaining number, √3 + √6.

So, the simplified form of the square root of 33 is √(9 × 3 + 6) = 3√(3 + 2/3).

Common Mistakes When Simplifying Radicals

When simplifying radicals, it's easy to make mistakes. Here are some common errors to watch out for:

• Not factoring out perfect squares: Make sure to identify and factor out perfect squares from the radicand.
• Not simplifying the radical: Don't forget to take the square root of the perfect square and multiply it by the remaining number.
• Adding or subtracting instead of multiplying: When simplifying radicals, you need to multiply the square root of the perfect square by the remaining number, not add or subtract.

Real-World Applications of Simplifying Radicals

Simplifying radicals has many real-world applications, including:

• Physics and engineering: Simplifying radicals is crucial in calculating distances, velocities, and accelerations in physics and engineering.
• Computer science: Radicals are used in computer science to calculate distances and angles in graphics and game development.
• Finance: Simplifying radicals is used in finance to calculate interest rates and investment returns.

Conclusion: Simplifying Radicals Made Easy

Simplifying radicals may seem daunting at first, but with practice and patience, it becomes easier. By following the steps outlined in this article and avoiding common mistakes, you'll become a pro at simplifying radicals in no time.

Now it's your turn! Try simplifying the square root of 33 on your own and see how it goes. If you have any questions or need further clarification, leave a comment below. Don't forget to share this article with your friends and family who love math as much as you do.