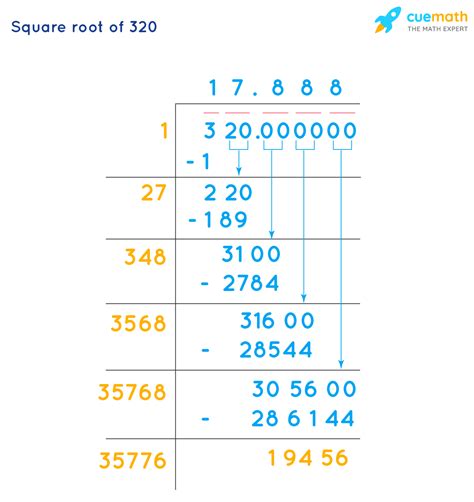
The square root of 320 is a value that, when multiplied by itself, gives the result of 320. To simplify the square root of 320, we need to find the factors of 320 that are perfect squares.
Breaking Down 320 into Prime Factors
To simplify the square root of 320, we start by breaking down 320 into its prime factors. This will help us identify the perfect square factors that we can take out of the square root.

The prime factorization of 320 is:
320 = 2 × 2 × 2 × 2 × 2 × 2 × 5
Identifying Perfect Square Factors
From the prime factorization of 320, we can see that there are multiple factors of 2, which is a perfect square. We can group these factors together to simplify the square root.

Grouping the perfect square factors together, we get:
√320 = √(2 × 2 × 2 × 2 × 2 × 2 × 5) = √(2^6 × 5) = √(64 × 5) = √64 × √5 = 8√5
Simplified Square Root of 320
The simplified square root of 320 in radical form is:
√320 = 8√5
This means that the square root of 320 can be expressed as 8 times the square root of 5.
Benefits of Simplifying the Square Root of 320
Simplifying the square root of 320 has several benefits, including:
- Easier calculations: Simplifying the square root of 320 makes it easier to perform calculations involving this value.
- Improved accuracy: By expressing the square root of 320 in simplified form, we can reduce the risk of errors and improve accuracy.
- Better understanding: Simplifying the square root of 320 helps us understand the underlying factors and relationships between numbers.

Real-World Applications of Simplifying the Square Root of 320
Simplifying the square root of 320 has several real-world applications, including:
- Science and engineering: Simplifying the square root of 320 is essential in various scientific and engineering applications, such as calculating distances, velocities, and accelerations.
- Finance: Simplifying the square root of 320 is used in finance to calculate interest rates, investment returns, and other financial metrics.
- Education: Simplifying the square root of 320 is an essential skill for students to learn, as it helps them understand mathematical concepts and solve problems.

Conclusion
In conclusion, simplifying the square root of 320 is an essential skill that has several benefits and real-world applications. By breaking down 320 into its prime factors and identifying perfect square factors, we can simplify the square root of 320 to 8√5. This simplified form makes it easier to perform calculations, improves accuracy, and helps us understand the underlying factors and relationships between numbers.

We hope this article has helped you understand the concept of simplifying the square root of 320. If you have any questions or comments, please feel free to share them below.
What is the simplified square root of 320?
+The simplified square root of 320 is 8√5.
Why is simplifying the square root of 320 important?
+Simplifying the square root of 320 makes it easier to perform calculations, improves accuracy, and helps us understand the underlying factors and relationships between numbers.
What are the real-world applications of simplifying the square root of 320?
+Simplifying the square root of 320 has several real-world applications, including science and engineering, finance, and education.