Square Root Of 180 In Radical Form Explained

Quick Links :

The square root of 180 is a mathematical concept that has been a subject of interest for many students and professionals alike. In this article, we will delve into the world of radicals and explore the square root of 180 in its radical form.

Mathematics is a fascinating field that deals with numbers, quantities, and shapes. It is a language that helps us understand the world around us, from the intricate patterns of nature to the complex systems of technology. One of the fundamental concepts in mathematics is the square root, which is a mathematical operation that finds the number that, when multiplied by itself, gives a specified value. In this article, we will focus on the square root of 180 and its radical form.

What is the Square Root of 180?

The square root of 180 is a number that, when multiplied by itself, gives 180. This number can be expressed in both integer and radical forms. The integer form of the square root of 180 is not a whole number, as 180 is not a perfect square. However, we can express it in radical form, which is a more precise and elegant way of representing this value.

How to Calculate the Square Root of 180

To calculate the square root of 180, we can use various methods, including the long division method, the prime factorization method, or a calculator. However, in this article, we will focus on the radical form, which provides a more intuitive and visual representation of this value.

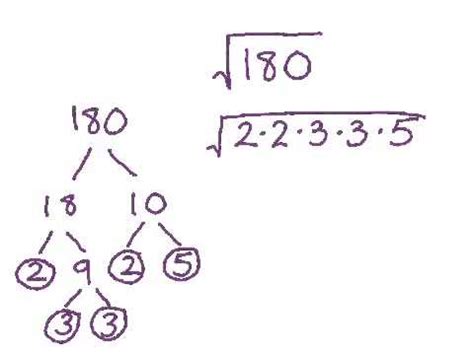
The prime factorization of 180 is 2^2 × 3^2 × 5. To find the square root of 180, we take the square root of each factor:

√180 = √(2^2 × 3^2 × 5) = √(2^2) × √(3^2) × √5 = 2 × 3 × √5 = 6√5

Therefore, the square root of 180 in radical form is 6√5.

Properties of the Square Root of 180

The square root of 180 has several properties that make it an interesting and useful mathematical concept. Some of these properties include:

• The square root of 180 is an irrational number, which means it cannot be expressed as a finite decimal or fraction.
• The square root of 180 is a real number, which means it is a value that exists on the real number line.
• The square root of 180 is a positive value, as the square of any real number is always positive.

Applications of the Square Root of 180

The square root of 180 has several applications in mathematics, science, and engineering. Some of these applications include:

• Geometry: The square root of 180 is used in geometry to calculate the length of the diagonal of a rectangle with a width of 6 and a height of 5.
• Trigonometry: The square root of 180 is used in trigonometry to calculate the sine and cosine of angles.
• Physics: The square root of 180 is used in physics to calculate the velocity of objects in motion.

Conclusion

In this article, we explored the square root of 180 in radical form. We calculated the value using prime factorization and discussed its properties and applications. The square root of 180 is an important mathematical concept that has numerous applications in mathematics, science, and engineering.

Final Thoughts

We hope this article has provided you with a deeper understanding of the square root of 180 in radical form. Whether you are a student, teacher, or simply a mathematics enthusiast, we encourage you to continue exploring the fascinating world of mathematics.