Simplifying Square Root Of 162 Radical Form

Quick Links :

The square root of 162 can be a daunting task for many, especially when dealing with radical forms. However, with the right approach, simplifying this expression can be a breeze. In this article, we will delve into the world of square roots, explore the concept of radical forms, and provide a step-by-step guide on how to simplify the square root of 162.

Understanding Square Roots and Radical Forms

Before we dive into the simplification process, it's essential to understand the basics of square roots and radical forms. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16.

Radical forms, on the other hand, are used to represent square roots in a more concise and mathematical way. The radical sign (√) is used to indicate the square root of a number. For instance, √16 represents the square root of 16, which is 4.

Simplifying the Square Root of 162

Now that we have a basic understanding of square roots and radical forms, let's move on to simplifying the square root of 162.

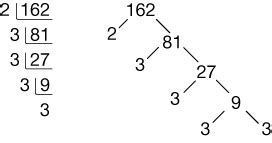
The square root of 162 can be expressed as √162. To simplify this expression, we need to find the factors of 162 that are perfect squares.

Prime Factorization of 162

To find the perfect square factors of 162, we need to perform prime factorization. Prime factorization involves breaking down a number into its prime factors.

The prime factorization of 162 is:

162 = 2 × 3 × 3 × 3 × 3

Finding Perfect Square Factors

Now that we have the prime factorization of 162, we can identify the perfect square factors. A perfect square factor is a factor that can be expressed as a square of an integer.

In this case, we can see that 9 is a perfect square factor of 162, since 9 = 3 × 3.

Simplifying the Square Root of 162

Now that we have identified the perfect square factor of 162, we can simplify the square root expression.

√162 = √(9 × 18)

Using the property of square roots, we can rewrite the expression as:

√162 = √9 × √18

Since √9 = 3, we can simplify further:

√162 = 3√18

Simplifying the Square Root of 18

To simplify the square root of 18, we need to find the perfect square factors of 18.

The prime factorization of 18 is:

18 = 2 × 3 × 3

We can see that 9 is a perfect square factor of 18, since 9 = 3 × 3.

Simplifying the Square Root of 18

Now that we have identified the perfect square factor of 18, we can simplify the square root expression.

√18 = √(9 × 2)

Using the property of square roots, we can rewrite the expression as:

√18 = √9 × √2

Since √9 = 3, we can simplify further:

√18 = 3√2

Final Simplification

Now that we have simplified the square root of 18, we can substitute this expression back into the original equation.

√162 = 3√18

Substituting √18 = 3√2, we get:

√162 = 3(3√2)

Simplifying further, we get:

√162 = 9√2

Conclusion

In conclusion, simplifying the square root of 162 radical form involves finding the perfect square factors of 162, simplifying the square root expression, and substituting the simplified expression back into the original equation. By following these steps, we can simplify the square root of 162 to 9√2.

Practical Applications

Simplifying square roots and radical forms has numerous practical applications in various fields, including mathematics, physics, engineering, and computer science. Understanding how to simplify these expressions can help you solve complex problems and equations more efficiently.

Tips and Tricks

Here are some tips and tricks to help you simplify square roots and radical forms:

• Always look for perfect square factors when simplifying square root expressions.
• Use prime factorization to break down numbers into their prime factors.
• Simplify square root expressions step by step, using the properties of square roots.
• Practice simplifying different types of square root expressions to improve your skills.

FAQs

We hope this article has helped you understand how to simplify the square root of 162 radical form. If you have any questions or comments, please feel free to share them below.