Simplifying square roots is an essential skill in mathematics, particularly in algebra and geometry. It involves expressing a square root in its simplest form, also known as radical form. In this article, we'll explore three easy ways to simplify square roots and convert them to radical form.
What are Square Roots?

A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. Square roots are denoted by the symbol √, and they play a crucial role in various mathematical operations.
Why Simplify Square Roots?

Simplifying square roots is essential because it helps to:
- Reduce complex expressions to their simplest form
- Make calculations easier and more accurate
- Improve problem-solving skills in mathematics
- Enhance understanding of mathematical concepts
Method 1: Simplifying Square Roots using Perfect Squares

One way to simplify square roots is to look for perfect squares that can be factored out of the expression. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. For example:
√16 = √(4 × 4) = 4
√25 = √(5 × 5) = 5
To simplify a square root using perfect squares:
- Look for perfect squares that can be factored out of the expression.
- Write the perfect square as a product of an integer multiplied by itself.
- Simplify the expression by taking the square root of the perfect square.
Example:
Simplify √48.
- Look for perfect squares that can be factored out of 48: 48 = 16 × 3
- Write 16 as a perfect square: 16 = 4 × 4
- Simplify the expression: √48 = √(16 × 3) = 4√3
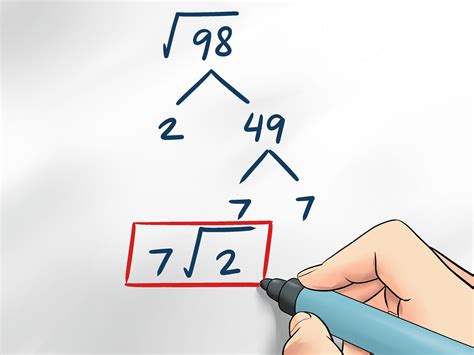
Method 2: Simplifying Square Roots using Prime Factorization

Another way to simplify square roots is to use prime factorization. Prime factorization involves breaking down a number into its prime factors, which are the building blocks of that number.
To simplify a square root using prime factorization:
- Factor the number into its prime factors.
- Identify pairs of identical prime factors.
- Simplify the expression by taking the square root of the paired prime factors.
Example:
Simplify √72.
- Factor 72 into its prime factors: 72 = 2 × 2 × 2 × 3 × 3
- Identify pairs of identical prime factors: 2 × 2 × 3 × 3
- Simplify the expression: √72 = √(2 × 2 × 3 × 3) = 6√2
Method 3: Simplifying Square Roots using the Conjugate Pair

The conjugate pair method involves simplifying square roots by using a conjugate pair, which is a pair of numbers that have the same real part and opposite imaginary parts.
To simplify a square root using the conjugate pair:
- Identify the conjugate pair of the square root.
- Multiply the numerator and denominator of the expression by the conjugate pair.
- Simplify the expression by canceling out the common factors.
Example:
Simplify √(3 + √2).
- Identify the conjugate pair: 3 - √2
- Multiply the numerator and denominator by the conjugate pair: √(3 + √2) × (3 - √2) / (3 - √2)
- Simplify the expression: √(9 - 2) = √7
Conclusion
Simplifying square roots is a crucial skill in mathematics that can be achieved using three easy methods: perfect squares, prime factorization, and the conjugate pair. By mastering these methods, you can simplify complex expressions, improve problem-solving skills, and enhance your understanding of mathematical concepts.
What is the purpose of simplifying square roots?
+Simplifying square roots is essential because it helps to reduce complex expressions to their simplest form, making calculations easier and more accurate, and improving problem-solving skills in mathematics.
What are the three methods for simplifying square roots?
+The three methods for simplifying square roots are: 1) using perfect squares, 2) using prime factorization, and 3) using the conjugate pair.
What is prime factorization?
+Prime factorization involves breaking down a number into its prime factors, which are the building blocks of that number.