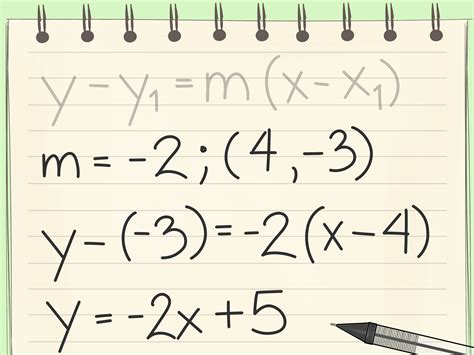The slope-intercept form, a fundamental concept in algebra and mathematics, is a powerful tool for understanding linear equations and their graphical representations. Mastering this form is essential for students and professionals alike, as it provides a versatile framework for solving problems, modeling real-world phenomena, and making informed decisions. In this article, we will delve into the world of slope-intercept form, exploring its definition, benefits, and practical applications.

Understanding the Slope-Intercept Form
The slope-intercept form is a way of expressing linear equations in the format y = mx + b, where:
- m represents the slope of the line, indicating the rate of change between the x and y variables.
- b represents the y-intercept, or the point at which the line crosses the y-axis.
- x and y are the variables, with x typically representing the input or independent variable, and y representing the output or dependent variable.
This form provides a concise and intuitive way to represent linear relationships, making it easier to analyze, graph, and solve equations.
Benefits of the Slope-Intercept Form
The slope-intercept form offers several advantages over other forms of linear equations, including:
- Simplified graphing: The slope-intercept form makes it easy to visualize the graph of a linear equation, as the slope and y-intercept provide valuable information about the line's orientation and position.
- Easy equation manipulation: The slope-intercept form allows for straightforward manipulation of the equation, enabling users to solve for one variable in terms of the other.
- Real-world applications: The slope-intercept form is commonly used in various fields, such as physics, engineering, economics, and finance, to model real-world phenomena and make predictions.
Method 1: Converting to Slope-Intercept Form
To master the slope-intercept form, it's essential to know how to convert other forms of linear equations into this format. Here are the steps:

- Start with the standard form: Begin with the standard form of a linear equation, ax + by = c.
- Isolate y: Rearrange the equation to isolate y, the dependent variable.
- Divide by the coefficient of y: Divide both sides of the equation by the coefficient of y (b) to solve for y.
- Simplify: Simplify the resulting equation to obtain the slope-intercept form, y = mx + b.
Example: Converting to Slope-Intercept Form
Convert the equation 2x + 3y = 5 to slope-intercept form:
- Isolate y: 3y = -2x + 5
- Divide by the coefficient of y: y = (-2/3)x + 5/3
- Simplify: y = (-2/3)x + 5/3
The resulting equation is in slope-intercept form, with a slope of -2/3 and a y-intercept of 5/3.
Method 2: Using the Slope-Intercept Form to Solve Equations
The slope-intercept form is particularly useful for solving linear equations, as it provides a straightforward method for finding the value of one variable in terms of the other.

- Write the equation in slope-intercept form: Express the equation in the format y = mx + b.
- Substitute values: Substitute the given values of x and y into the equation.
- Solve for the unknown variable: Solve for the unknown variable, either x or y, depending on the values given.
Example: Solving an Equation with Slope-Intercept Form
Solve the equation y = 2x + 1 when x = 3:
- Write the equation in slope-intercept form: y = 2x + 1
- Substitute values: y = 2(3) + 1
- Solve for y: y = 7
The value of y is 7 when x is 3.
Method 3: Graphing Linear Equations in Slope-Intercept Form
Graphing linear equations in slope-intercept form is a straightforward process, as the slope and y-intercept provide valuable information about the line's orientation and position.

- Plot the y-intercept: Plot the y-intercept, or the point at which the line crosses the y-axis.
- Use the slope to find another point: Use the slope to find another point on the line, either by moving up or down from the y-intercept.
- Draw the line: Draw the line through the two points, using a ruler or other straightedge.
Example: Graphing a Linear Equation in Slope-Intercept Form
Graph the equation y = 2x - 3:
- Plot the y-intercept: (0, -3)
- Use the slope to find another point: (1, -1)
- Draw the line: Draw the line through the points (0, -3) and (1, -1).
By following these steps, you can graph linear equations in slope-intercept form, making it easier to visualize and analyze the relationships between variables.
What is the slope-intercept form of a linear equation?
+The slope-intercept form is a way of expressing linear equations in the format y = mx + b, where m is the slope and b is the y-intercept.
How do I convert a standard form equation to slope-intercept form?
+To convert a standard form equation to slope-intercept form, isolate y, divide by the coefficient of y, and simplify the resulting equation.
What are the benefits of using the slope-intercept form?
+The slope-intercept form provides a concise and intuitive way to represent linear relationships, making it easier to analyze, graph, and solve equations.
By mastering the slope-intercept form, you'll be well-equipped to tackle a wide range of mathematical and real-world problems with confidence. Whether you're a student or a professional, this fundamental concept is an essential tool in your toolkit. So, take the time to practice and reinforce your understanding of the slope-intercept form, and you'll be solving linear equations and graphing lines like a pro in no time!