In mathematics, particularly in algebra and geometry, the concept of slope is crucial in understanding linear equations and their graphical representations. The slope-intercept form of a linear equation is a fundamental way to express the relationship between two variables, x and y. However, there's a specific scenario that often raises confusion among students and even some educators: an undefined slope in slope-intercept form. This article aims to clarify what an undefined slope means, its implications, and how it affects the slope-intercept form of a linear equation.
Understanding Slope-Intercept Form

Before diving into the concept of an undefined slope, let's first review the slope-intercept form of a linear equation. The slope-intercept form is expressed as:
y = mx + b
where:
- y is the dependent variable (the variable being predicted or explained)
- x is the independent variable (the variable being manipulated or controlled)
- m is the slope of the line (a measure of how steep the line is)
- b is the y-intercept (the point where the line intersects the y-axis)
The slope, m, represents the change in y for a one-unit change in x. In other words, it measures the rate at which y increases or decreases as x increases or decreases.
What is an Undefined Slope?
An undefined slope occurs when the denominator of the slope formula is equal to zero. The slope formula is:
m = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are two points on the line.
When the denominator (x2 - x1) is equal to zero, the slope is undefined because division by zero is undefined. This happens when the two points have the same x-coordinate, resulting in a vertical line.
Implications of an Undefined Slope

An undefined slope has significant implications for the slope-intercept form of a linear equation. Since the slope is undefined, the slope-intercept form cannot be applied in its standard form. This is because the slope-intercept form relies on the slope being a defined value.
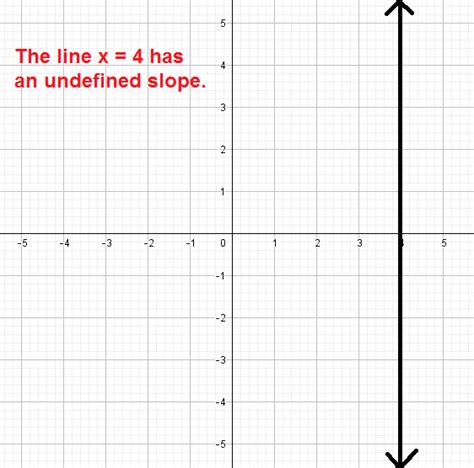
In the case of an undefined slope, the line is vertical, and its equation cannot be expressed in the slope-intercept form. Instead, the equation of a vertical line is expressed as:
x = a
where a is a constant value.
Key Differences between Undefined and Zero Slope
It's essential to distinguish between an undefined slope and a zero slope. A zero slope indicates that the line is horizontal, and its equation can be expressed in the slope-intercept form as:
y = b
where b is the y-intercept.
On the other hand, an undefined slope indicates that the line is vertical, and its equation cannot be expressed in the slope-intercept form.
Graphical Representation

The graphical representation of a line with an undefined slope is a vertical line. This line extends infinitely in the positive and negative y-directions, with a constant x-coordinate.
In contrast, a line with a zero slope is a horizontal line, extending infinitely in the positive and negative x-directions, with a constant y-coordinate.
Real-World Applications
Undefined slopes have practical applications in various fields, such as physics, engineering, and computer science. For instance, in physics, an undefined slope can represent a vertical asymptote in a graph, indicating a point of infinite density or a singularity.
In engineering, undefined slopes can be used to model real-world systems, such as a building's vertical structure or a bridge's vertical support.
Conclusion and Future Directions

In conclusion, an undefined slope in slope-intercept form is a fundamental concept in mathematics, indicating a vertical line with a constant x-coordinate. Understanding the implications and graphical representation of an undefined slope is crucial for solving linear equations and modeling real-world systems.
As we continue to explore the intricacies of linear equations and their applications, it's essential to remember that undefined slopes play a vital role in shaping our understanding of mathematical concepts and their practical applications.
We encourage you to share your thoughts and questions about undefined slopes in the comments section below. How have you encountered undefined slopes in your studies or real-world experiences? What challenges have you faced, and how have you overcome them?
What is the slope-intercept form of a linear equation?
+The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.
What is an undefined slope?
+An undefined slope occurs when the denominator of the slope formula is equal to zero, resulting in a vertical line.
What is the difference between an undefined slope and a zero slope?
+An undefined slope indicates a vertical line, while a zero slope indicates a horizontal line.