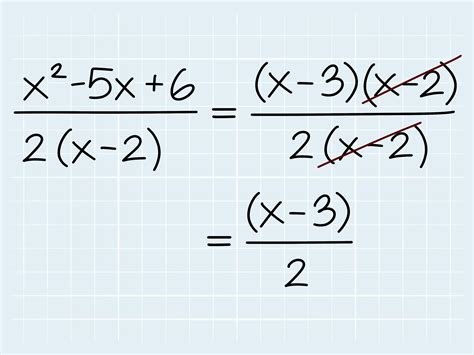Simplifying Algebraic Expressions: A Comprehensive Guide

Algebraic expressions are a crucial part of mathematics, and simplifying them is an essential skill for anyone who wants to master the subject. In this article, we will explore the world of algebraic expressions and provide you with a step-by-step guide on how to simplify them easily. Whether you're a student, teacher, or simply a math enthusiast, this article will help you understand the concepts and techniques involved in simplifying algebraic expressions.
What are Algebraic Expressions?
Algebraic expressions are mathematical expressions that contain variables, constants, and mathematical operations. They can be simple or complex, depending on the number of variables, constants, and operations involved. Algebraic expressions are used to represent relationships between variables and are a fundamental part of algebra.
Why Simplify Algebraic Expressions?

Simplifying algebraic expressions is essential for several reasons:
- It makes it easier to understand and work with the expression.
- It helps to identify patterns and relationships between variables.
- It enables us to solve equations and inequalities more efficiently.
- It reduces errors and makes calculations more accurate.
Basic Rules for Simplifying Algebraic Expressions

Before we dive into the step-by-step guide, let's review some basic rules for simplifying algebraic expressions:
- Combine like terms: Combine constants with constants and variables with variables.
- Use the distributive property: Expand expressions using the distributive property.
- Cancel out common factors: Cancel out common factors between the numerator and denominator.
- Simplify fractions: Simplify fractions by canceling out common factors.
Step-by-Step Guide to Simplifying Algebraic Expressions

Now that we've reviewed the basic rules, let's move on to the step-by-step guide:
- Read and understand the expression: Read the expression carefully and understand what's being asked.
- Combine like terms: Combine constants with constants and variables with variables.
- Use the distributive property: Expand expressions using the distributive property.
- Cancel out common factors: Cancel out common factors between the numerator and denominator.
- Simplify fractions: Simplify fractions by canceling out common factors.
- Check for any remaining simplifications: Check if there are any remaining simplifications that can be made.
Examples of Simplifying Algebraic Expressions

Let's look at some examples of simplifying algebraic expressions:
- Example 1: Simplify the expression 2x + 5 + 3x - 2.
- Combine like terms: 2x + 3x = 5x and 5 - 2 = 3.
- Simplified expression: 5x + 3.
- Example 2: Simplify the expression (2x + 5)(3x - 2).
- Use the distributive property: 2x(3x - 2) + 5(3x - 2).
- Expand the expression: 6x^2 - 4x + 15x - 10.
- Combine like terms: 6x^2 + 11x - 10.
- Example 3: Simplify the expression (2x + 5)/(3x - 2).
- Cancel out common factors: (2x + 5)/(3x - 2) = (2x + 5)/(3(x - 2/3)).
- Simplify the fraction: (2x + 5)/(3(x - 2/3)) = (2x + 5)/3(x - 2/3).
Common Mistakes to Avoid

When simplifying algebraic expressions, there are several common mistakes to avoid:
- Not combining like terms: Failing to combine like terms can lead to incorrect simplifications.
- Not using the distributive property: Failing to use the distributive property can lead to incorrect expansions.
- Not canceling out common factors: Failing to cancel out common factors can lead to incorrect simplifications.
- Not simplifying fractions: Failing to simplify fractions can lead to incorrect simplifications.
Conclusion
Simplifying algebraic expressions is an essential skill for anyone who wants to master algebra. By following the step-by-step guide and avoiding common mistakes, you can simplify algebraic expressions easily and accurately. Remember to always read and understand the expression, combine like terms, use the distributive property, cancel out common factors, simplify fractions, and check for any remaining simplifications.
Call to Action
We hope this article has helped you understand the concepts and techniques involved in simplifying algebraic expressions. If you have any questions or need further clarification, please don't hesitate to ask. Share this article with your friends and colleagues who may benefit from it. Happy learning!
What is the importance of simplifying algebraic expressions?
+Simplifying algebraic expressions is essential for several reasons: it makes it easier to understand and work with the expression, helps to identify patterns and relationships between variables, enables us to solve equations and inequalities more efficiently, and reduces errors and makes calculations more accurate.
What are the basic rules for simplifying algebraic expressions?
+The basic rules for simplifying algebraic expressions are: combine like terms, use the distributive property, cancel out common factors, and simplify fractions.
How can I avoid common mistakes when simplifying algebraic expressions?
+To avoid common mistakes when simplifying algebraic expressions, make sure to combine like terms, use the distributive property, cancel out common factors, and simplify fractions. Also, always read and understand the expression carefully before attempting to simplify it.