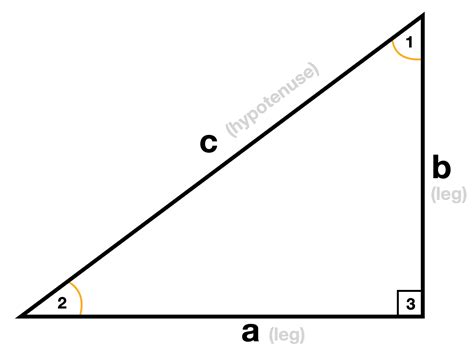
Right triangles are one of the most fundamental concepts in geometry, and understanding their side lengths is crucial for various mathematical and real-world applications. In this comprehensive guide, we'll delve into the world of right triangles, exploring the different types, formulas, and calculators to help you master this essential topic.
Right triangles are characterized by one right angle (90 degrees) and two acute angles (less than 90 degrees). The side opposite the right angle is called the hypotenuse, while the other two sides are known as legs. Understanding the relationships between these side lengths is vital for solving various problems in mathematics, physics, engineering, and more.

Pythagorean Theorem: The Foundation of Right Triangles
The Pythagorean theorem is a fundamental concept in geometry that describes the relationship between the side lengths of a right triangle. The theorem states that:
a² + b² = c²
where a and b are the lengths of the legs, and c is the length of the hypotenuse. This theorem is essential for calculating the length of the hypotenuse or finding the length of a leg when the other leg and hypotenuse are known.
Example: Finding the Hypotenuse
Suppose we have a right triangle with legs of length 3 and 4. To find the length of the hypotenuse, we can use the Pythagorean theorem:
3² + 4² = c² 9 + 16 = c² 25 = c² c = √25 c = 5
Therefore, the length of the hypotenuse is 5.
Special Right Triangles: 30-60-90 and 45-45-90
There are two special types of right triangles that have unique properties: 30-60-90 and 45-45-90 triangles. These triangles have specific ratios between their side lengths, making them useful for solving various problems.

30-60-90 Triangles
In a 30-60-90 triangle, the side opposite the 30-degree angle is half the length of the hypotenuse, while the side opposite the 60-degree angle is √3 times the length of the shorter leg.
45-45-90 Triangles
In a 45-45-90 triangle, the two legs are equal in length, and the hypotenuse is √2 times the length of a leg.
Right Triangle Calculator: A Handy Tool
To make calculations easier, we've created a right triangle calculator that can help you find the length of the hypotenuse or legs. Simply enter the known values, and the calculator will do the rest.

How to Use the Calculator
- Choose the type of calculation you want to perform (find hypotenuse or find leg).
- Enter the known values (either two legs or one leg and hypotenuse).
- Click the "Calculate" button to get the result.
Real-World Applications of Right Triangles
Right triangles have numerous applications in various fields, including:
Physics and Engineering
Right triangles are used to calculate distances, velocities, and forces in physics and engineering. For example, the trajectory of a projectile can be modeled using a right triangle.
Architecture and Construction
Right triangles are essential in architecture and construction, where they're used to calculate distances, heights, and angles.
Navigation and Surveying
Right triangles are used in navigation and surveying to calculate distances and angles between landmarks.

Conclusion and Call to Action
Mastering right triangles is a fundamental skill that can benefit you in various mathematical and real-world applications. With the Pythagorean theorem, special right triangles, and our handy calculator, you're equipped to tackle a wide range of problems. Take the next step by practicing with sample problems and exploring the many applications of right triangles.
What's your favorite way to apply right triangles in real-life situations? Share your thoughts and examples in the comments below!
What is the Pythagorean theorem?
+The Pythagorean theorem is a fundamental concept in geometry that describes the relationship between the side lengths of a right triangle. It states that a² + b² = c², where a and b are the lengths of the legs, and c is the length of the hypotenuse.
What is a special right triangle?
+A special right triangle is a right triangle with unique properties, such as the 30-60-90 and 45-45-90 triangles. These triangles have specific ratios between their side lengths, making them useful for solving various problems.
How do I use the right triangle calculator?
+To use the right triangle calculator, simply choose the type of calculation you want to perform (find hypotenuse or find leg), enter the known values (either two legs or one leg and hypotenuse), and click the "Calculate" button to get the result.