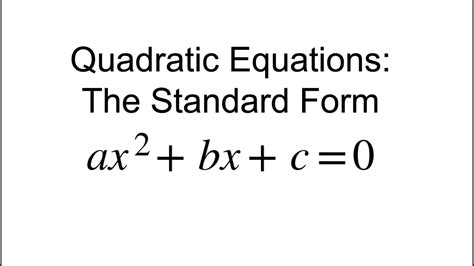Understanding Quadratic Functions and Their Importance

Quadratic functions are a fundamental concept in algebra and are used to model a wide range of real-world phenomena, from the trajectory of a projectile to the growth of a population. A quadratic function is a polynomial function of degree two, which means the highest power of the variable is two. In this article, we will explore the concept of quadratic functions in standard form and provide a step-by-step guide on how to easily rewrite them.
Quadratic functions are essential in various fields, including physics, engineering, economics, and computer science. They are used to model complex relationships between variables and make predictions about future outcomes. Understanding quadratic functions is crucial for solving problems in these fields and making informed decisions.
What is Standard Form?

The standard form of a quadratic function is a way of expressing the function in a specific format, which makes it easier to analyze and solve. The standard form of a quadratic function is:
ax^2 + bx + c
where a, b, and c are constants, and x is the variable. The coefficient "a" cannot be zero, and the expression is typically written in the order of descending powers of x.
Why is Standard Form Important?
The standard form of a quadratic function is important because it allows us to easily identify the key features of the function, such as the vertex, axis of symmetry, and x-intercepts. It also makes it easier to solve the function using various methods, such as factoring, quadratic formula, and graphing.
Rewriting Quadratic Functions in Standard Form

Rewriting a quadratic function in standard form involves rearranging the terms to match the standard form format. Here are the steps to follow:
- Combine like terms: Combine any like terms in the function, such as the x^2 terms or the constant terms.
- Rearrange the terms: Rearrange the terms to match the standard form format, with the x^2 term first, followed by the x term, and then the constant term.
- Check the coefficient: Check that the coefficient of the x^2 term is not zero. If it is, the function is not a quadratic function.
Example 1: Rewriting a Quadratic Function in Standard Form
Suppose we have the quadratic function:
x^2 + 4x + 3 = 0
To rewrite this function in standard form, we need to combine like terms and rearrange the terms:
x^2 + 4x + 3 = 0
Combine like terms:
x^2 + 4x + 3 = 0
Rearrange the terms:
x^2 + 4x + 3 = 0
Check the coefficient:
The coefficient of the x^2 term is 1, which is not zero.
Therefore, the quadratic function in standard form is:
x^2 + 4x + 3
Practical Applications of Quadratic Functions in Standard Form

Quadratic functions in standard form have numerous practical applications in various fields, including:
- Projectile motion: Quadratic functions are used to model the trajectory of a projectile, such as the path of a thrown ball or a launched rocket.
- Economics: Quadratic functions are used to model the relationship between the price of a good and the quantity demanded or supplied.
- Computer science: Quadratic functions are used in algorithms for solving problems, such as finding the shortest path between two points.
Example 2: Using Quadratic Functions in Standard Form to Model Projectile Motion
Suppose we want to model the trajectory of a thrown ball. We can use a quadratic function in standard form to represent the height of the ball as a function of time:
h(t) = -16t^2 + 64t + 10
where h(t) is the height of the ball at time t, and t is the time in seconds.
This function represents the height of the ball as a parabola, with the vertex at the maximum height of 40 feet.
Conclusion

In conclusion, quadratic functions in standard form are a fundamental concept in algebra and have numerous practical applications in various fields. By following the steps outlined in this article, you can easily rewrite quadratic functions in standard form and apply them to solve problems in physics, engineering, economics, and computer science.
We hope this article has provided you with a comprehensive understanding of quadratic functions in standard form and has inspired you to explore the many practical applications of these functions.
What do you think? Share your thoughts and comments below!
What is the standard form of a quadratic function?
+The standard form of a quadratic function is ax^2 + bx + c, where a, b, and c are constants, and x is the variable.
Why is standard form important?
+Standard form is important because it allows us to easily identify the key features of the function, such as the vertex, axis of symmetry, and x-intercepts.
How do I rewrite a quadratic function in standard form?
+To rewrite a quadratic function in standard form, combine like terms, rearrange the terms to match the standard form format, and check that the coefficient of the x^2 term is not zero.