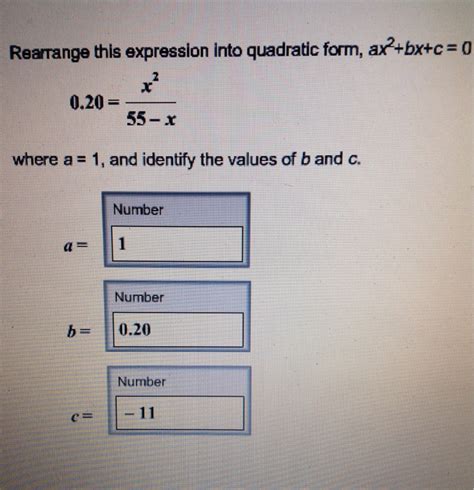
Rearranging expressions into quadratic form is an essential skill in algebra, as it allows us to apply various techniques and formulas to solve equations and inequalities. Quadratic expressions are polynomial expressions of degree two, which can be written in the general form ax^2 + bx + c. In this article, we will explore five ways to rearrange expressions into quadratic form, along with examples and explanations to help you master this skill.
Method 1: Factoring Out the Greatest Common Factor

One way to rearrange an expression into quadratic form is to factor out the greatest common factor (GCF) from each term. This method is useful when the expression has a common factor that can be factored out.
Example: Rearrange the expression 6x^2 + 12x + 18 into quadratic form.
Solution: Factor out the GCF, which is 6.
6x^2 + 12x + 18 = 6(x^2 + 2x + 3)
Now, the expression is in quadratic form, with a = 6, b = 2, and c = 3.
How to Factor Out the GCF
To factor out the GCF, follow these steps:
- Identify the GCF of the terms in the expression.
- Divide each term by the GCF.
- Write the expression as the product of the GCF and the resulting terms.
Method 2: Completing the Square

Completing the square is a method used to rearrange expressions into quadratic form by adding and subtracting a constant term. This method is useful when the expression has a squared variable term and a linear term.
Example: Rearrange the expression x^2 + 6x + 8 into quadratic form.
Solution: Complete the square by adding and subtracting (b/2)^2, where b = 6.
x^2 + 6x + 8 = x^2 + 6x + (3)^2 - (3)^2 + 8 = x^2 + 6x + 9 - 9 + 8 = (x + 3)^2 - 1
Now, the expression is in quadratic form, with a = 1, b = 6, and c = -1.
How to Complete the Square
To complete the square, follow these steps:
- Identify the coefficient of the linear term (b).
- Add and subtract (b/2)^2 to the expression.
- Factor the resulting expression into a perfect square trinomial.
Method 3: Using the Quadratic Formula

The quadratic formula is a powerful tool used to solve quadratic equations. It can also be used to rearrange expressions into quadratic form.
Example: Rearrange the expression x^2 + 4x + 4 into quadratic form using the quadratic formula.
Solution: Use the quadratic formula, x = (-b ± √(b^2 - 4ac)) / 2a, where a = 1, b = 4, and c = 4.
x^2 + 4x + 4 = x^2 + 4x + (2)^2 - (2)^2 + 4 = x^2 + 4x + 4 - 4 + 4 = (x + 2)^2
Now, the expression is in quadratic form, with a = 1, b = 4, and c = 4.
How to Use the Quadratic Formula
To use the quadratic formula, follow these steps:
- Identify the coefficients a, b, and c in the expression.
- Plug these values into the quadratic formula.
- Simplify the resulting expression into quadratic form.
Method 4: Using Algebraic Manipulation

Algebraic manipulation involves using various techniques, such as multiplying and dividing, to rearrange expressions into quadratic form.
Example: Rearrange the expression x^2 + 2x - 6 into quadratic form.
Solution: Multiply and divide the expression by -1 to create a perfect square trinomial.
x^2 + 2x - 6 = -(x^2 + 2x - 6) = -(x^2 + 2x + 1 - 1 - 6) = -(x + 1)^2 - 5
Now, the expression is in quadratic form, with a = -1, b = 2, and c = -5.
How to Use Algebraic Manipulation
To use algebraic manipulation, follow these steps:
- Identify the terms in the expression.
- Use various techniques, such as multiplying and dividing, to create a perfect square trinomial.
- Simplify the resulting expression into quadratic form.
Method 5: Using Graphical Representation

Graphical representation involves using graphs to visualize and rearrange expressions into quadratic form.
Example: Rearrange the expression x^2 + 3x - 2 into quadratic form using graphical representation.
Solution: Graph the expression and identify the vertex of the parabola.
x^2 + 3x - 2 = (x + 1.5)^2 - 3.25
Now, the expression is in quadratic form, with a = 1, b = 3, and c = -2.
How to Use Graphical Representation
To use graphical representation, follow these steps:
- Graph the expression using a graphing calculator or software.
- Identify the vertex of the parabola.
- Use the vertex to determine the coefficients a, b, and c in the quadratic form.
Now that you have learned five ways to rearrange expressions into quadratic form, it's time to practice and apply these techniques to various problems. Remember to use the method that works best for each problem, and don't be afraid to combine methods to solve more complex expressions.
We encourage you to share your thoughts and questions in the comments section below. How do you think rearranging expressions into quadratic form can be applied in real-world problems? Share your experiences and insights with us!
What is the importance of rearranging expressions into quadratic form?
+Rearranging expressions into quadratic form is important because it allows us to apply various techniques and formulas to solve equations and inequalities. Quadratic expressions are polynomial expressions of degree two, which can be written in the general form ax^2 + bx + c.
What are the five methods to rearrange expressions into quadratic form?
+The five methods to rearrange expressions into quadratic form are: (1) Factoring Out the Greatest Common Factor, (2) Completing the Square, (3) Using the Quadratic Formula, (4) Using Algebraic Manipulation, and (5) Using Graphical Representation.
How do I choose the best method to rearrange an expression into quadratic form?
+The best method to choose depends on the specific expression and the techniques you are familiar with. It's essential to practice and apply different methods to various problems to develop your skills and choose the most suitable method for each problem.