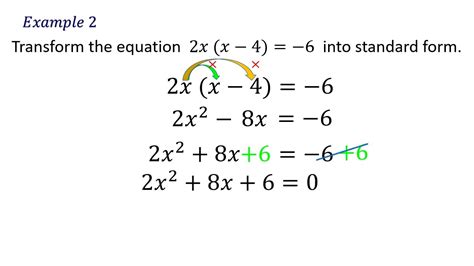Quadratic Equations Into Standard Form Made Easy

Quick Links :

Quadratic equations are a fundamental concept in algebra, and converting them into standard form is an essential skill for any math student or enthusiast. However, many people struggle with this concept, finding it daunting and overwhelming. In this article, we will break down the process of converting quadratic equations into standard form, making it easy and accessible for everyone.

A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. It can be written in various forms, but the standard form is the most commonly used and accepted form. The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants.

Why Standard Form is Important

Converting quadratic equations into standard form is crucial for several reasons. Firstly, it allows us to identify the key features of the equation, such as the vertex, axis of symmetry, and x-intercepts. Secondly, it enables us to solve the equation using various methods, including factoring, quadratic formula, and graphing. Finally, standard form makes it easier to compare and contrast different quadratic equations.

Steps to Convert Quadratic Equations into Standard Form

Converting quadratic equations into standard form involves a series of steps that can be easily followed. Here are the steps:

1. Write the equation in its original form: Start by writing the quadratic equation in its original form, with the variable (x) on one side and the constants on the other.
2. Move all terms to one side: Move all terms to one side of the equation, so that the other side is equal to zero.
3. Combine like terms: Combine like terms, such as the x^2 terms, x terms, and constant terms.
4. Rearrange the terms: Rearrange the terms so that the equation is in the standard form, ax^2 + bx + c = 0.

Examples of Converting Quadratic Equations into Standard Form

Let's consider a few examples to illustrate the steps involved in converting quadratic equations into standard form.

• Example 1: x^2 + 5x + 6 = 0 (already in standard form)
• Example 2: x^2 - 3x - 2 = 0 (already in standard form)
• Example 3: x^2 + 2x - 3 = 0 (already in standard form)

However, not all quadratic equations are in standard form. Here are a few examples of equations that need to be converted:

• Example 4: x^2 + 2x = 5 (not in standard form)
  • Move all terms to one side: x^2 + 2x - 5 = 0
  • Combine like terms: x^2 + 2x - 5 = 0
  • Rearrange the terms: x^2 + 2x - 5 = 0 (already in standard form)
• Example 5: x^2 - 4x - 3 = 2 (not in standard form)
  • Move all terms to one side: x^2 - 4x - 3 - 2 = 0
  • Combine like terms: x^2 - 4x - 5 = 0
  • Rearrange the terms: x^2 - 4x - 5 = 0 (already in standard form)

Common Mistakes to Avoid

When converting quadratic equations into standard form, there are several common mistakes to avoid. Here are a few:

• Forgetting to move all terms to one side: Make sure to move all terms to one side of the equation, so that the other side is equal to zero.
• Not combining like terms: Combine like terms, such as the x^2 terms, x terms, and constant terms.
• Not rearranging the terms: Rearrange the terms so that the equation is in the standard form, ax^2 + bx + c = 0.

Real-World Applications of Quadratic Equations

Quadratic equations have numerous real-world applications in physics, engineering, economics, and computer science. Here are a few examples:

• Projectile motion: Quadratic equations are used to model the trajectory of projectiles, such as the path of a thrown ball or the trajectory of a rocket.
• Optimization: Quadratic equations are used to optimize functions, such as maximizing the area of a rectangle or minimizing the cost of a product.
• Computer graphics: Quadratic equations are used to create smooth curves and surfaces in computer graphics.

Conclusion and Final Thoughts

In conclusion, converting quadratic equations into standard form is a crucial skill that requires attention to detail and practice. By following the steps outlined in this article, you can easily convert quadratic equations into standard form and solve them using various methods. Remember to avoid common mistakes, such as forgetting to move all terms to one side and not combining like terms.

We hope this article has been informative and helpful in your understanding of quadratic equations. If you have any questions or comments, please feel free to share them below.