5 Easy Ways To Prime Factorization Expanded Form

Quick Links :

The concept of prime factorization has been a cornerstone of mathematics for centuries, providing a fundamental understanding of numbers and their underlying structure. For many students and math enthusiasts, prime factorization is a fascinating topic that unlocks the secrets of numerical relationships. In this article, we will explore the concept of prime factorization in expanded form, highlighting its importance and providing five easy ways to master this essential math skill.

What is Prime Factorization?

Prime factorization is a mathematical process that involves breaking down a composite number into its prime factors. A prime number is a positive integer that is divisible only by itself and 1, such as 2, 3, 5, and 7. By finding the prime factors of a number, we can express it as a product of its prime factors in a unique way, known as the prime factorization.

Why is Prime Factorization Important?

Prime factorization has numerous applications in mathematics, science, and engineering. Some of the key reasons why prime factorization is important include:

• Simplifying complex calculations: Prime factorization can help simplify complex calculations by breaking down numbers into their prime factors.
• Understanding numerical relationships: Prime factorization provides insight into the underlying structure of numbers, revealing patterns and relationships that might not be immediately apparent.
• Cryptography: Prime factorization is used in cryptography to secure online transactions and communication.

5 Easy Ways to Prime Factorization Expanded Form

Method 1: Division Method

The division method is a straightforward approach to prime factorization. Here's how it works:

1. Divide the number by the smallest prime number, which is 2.
2. If the number is divisible, write down the prime factor and divide the result by the same prime number.
3. Repeat step 2 until the number is no longer divisible by the prime number.
4. Move on to the next prime number and repeat the process.

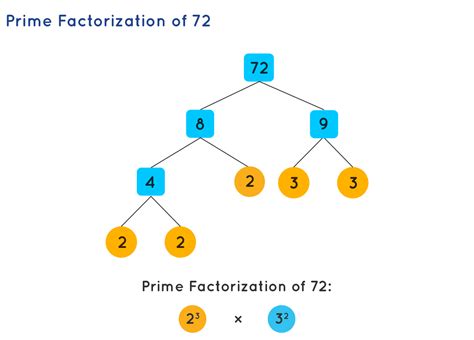
Method 2: Factor Tree Method

The factor tree method is a visual approach to prime factorization. Here's how it works:

1. Start with the number and draw a tree with two branches.
2. Write down the two factors of the number on the branches.
3. If the factors are not prime numbers, draw two more branches from each factor.
4. Continue this process until you reach the prime factors.

Method 3: Prime Factorization Chart

A prime factorization chart is a table that lists the prime factors of numbers. Here's how to use it:

1. Find the number in the chart and look up its prime factors.
2. Write down the prime factors and their exponents.

Method 4: Repeated Division Method

The repeated division method is a variation of the division method. Here's how it works:

1. Divide the number by the smallest prime number.
2. If the number is divisible, write down the prime factor and divide the result by the same prime number.
3. Repeat step 2 until the number is no longer divisible by the prime number.
4. Move on to the next prime number and repeat the process.

Method 5: Online Tools and Calculators

There are many online tools and calculators available that can help with prime factorization. Here's how to use them:

1. Enter the number into the calculator or tool.
2. Click the "prime factorization" button or option.
3. The tool will display the prime factors and their exponents.

Getting the Most Out of Prime Factorization

To get the most out of prime factorization, it's essential to practice regularly and use a combination of the methods outlined above. Here are some additional tips:

• Start with simple numbers: Begin with small numbers and work your way up to more complex ones.
• Use real-world examples: Apply prime factorization to real-world problems, such as calculating the greatest common divisor (GCD) of two numbers.
• Explore different methods: Experiment with different methods to find the one that works best for you.

Wrapping Up

Prime factorization is a fundamental math concept that has numerous applications in mathematics, science, and engineering. By mastering prime factorization in expanded form, you can simplify complex calculations, understand numerical relationships, and develop problem-solving skills. With the five easy methods outlined above, you can start exploring the world of prime factorization and unlock its many benefits.

We hope you found this article helpful and informative. If you have any questions or comments, please feel free to share them below. Don't forget to share this article with your friends and colleagues who may be interested in learning more about prime factorization.