Polar Form Of An Ellipse Explained

Quick Links :

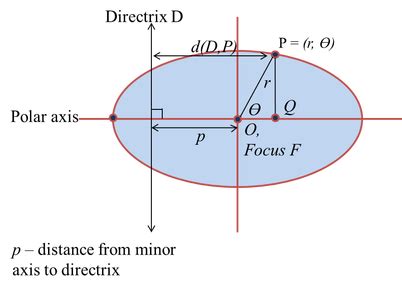
The polar form of an ellipse is a mathematical concept used to describe the shape of an ellipse in terms of its polar coordinates. Ellipses are common shapes in mathematics, physics, and engineering, and understanding their polar form is crucial for solving problems in these fields.

In mathematics, an ellipse is defined as the set of all points in a plane such that the sum of their distances from two fixed points (called the foci) is constant. This definition can be used to derive the equation of an ellipse in Cartesian coordinates, but it can also be expressed in polar coordinates.

Polar coordinates are a way of describing points in a plane using a distance from a reference point (called the origin) and an angle from a reference direction (called the polar axis). In polar coordinates, an ellipse can be described using a single equation, which makes it easier to analyze and solve problems involving ellipses.

Equation of an Ellipse in Polar Coordinates

The equation of an ellipse in polar coordinates is:

r = a(1 - e^2) / (1 + e * cos(θ))

where:

• r is the radial distance from the origin to a point on the ellipse
• a is the semi-major axis of the ellipse (the distance from the center to the farthest point on the ellipse)
• e is the eccentricity of the ellipse (a measure of how elliptical the shape is)
• θ is the polar angle (the angle between the polar axis and the line connecting the origin to the point on the ellipse)

Understanding the Equation

The equation of an ellipse in polar coordinates is a powerful tool for analyzing and solving problems involving ellipses. The equation shows that the radial distance from the origin to a point on the ellipse depends on the polar angle θ.

The term (1 - e^2) represents the distance from the center of the ellipse to the focus, while the term (1 + e * cos(θ)) represents the distance from the focus to the point on the ellipse. The product of these two terms gives the radial distance from the origin to the point on the ellipse.

Benefits of Using Polar Coordinates

Using polar coordinates to describe an ellipse has several benefits:

• Simplified equation: The equation of an ellipse in polar coordinates is simpler and more elegant than the equation in Cartesian coordinates.
• Easy analysis: The polar equation makes it easy to analyze the properties of the ellipse, such as its shape, size, and orientation.
• Efficient computation: Polar coordinates are more efficient for computing the position and velocity of objects moving along an elliptical path.

Applications of Polar Coordinates

Polar coordinates have many practical applications in physics, engineering, and computer science. Some examples include:

• Orbital mechanics: Polar coordinates are used to describe the motion of celestial bodies, such as planets and satellites, in orbit around a central body.
• Trajectory planning: Polar coordinates are used to plan the trajectory of vehicles, such as rockets and spacecraft, as they move along an elliptical path.
• Graphics and game development: Polar coordinates are used to create smooth and efficient animations of objects moving along an elliptical path.

Steps to Convert Cartesian to Polar Coordinates

To convert Cartesian coordinates (x, y) to polar coordinates (r, θ), follow these steps:

1. Calculate the radial distance r using the formula: r = √(x^2 + y^2)
2. Calculate the polar angle θ using the formula: θ = arctan(y/x)
3. Use the polar equation of the ellipse to find the value of r in terms of θ

Tips and Tricks

When working with polar coordinates, keep the following tips and tricks in mind:

• Use the correct units: Make sure to use the correct units for the radial distance and polar angle.
• Use the correct quadrant: Make sure to use the correct quadrant when calculating the polar angle.
• Simplify the equation: Simplify the polar equation of the ellipse to make it easier to work with.

Common Mistakes to Avoid

When working with polar coordinates, avoid the following common mistakes:

• Forgetting to convert Cartesian coordinates to polar coordinates
• Using the wrong formula for calculating the radial distance or polar angle
• Forgetting to simplify the polar equation of the ellipse

Conclusion

In conclusion, the polar form of an ellipse is a powerful tool for analyzing and solving problems involving ellipses. By understanding the equation of an ellipse in polar coordinates, you can simplify complex problems and gain insights into the properties of ellipses.

We hope this article has been informative and helpful. If you have any questions or comments, please don't hesitate to reach out. Share this article with your friends and colleagues who may be interested in learning more about polar coordinates and ellipses.