Converting polar coordinates to rectangular form is a crucial skill in mathematics, particularly in trigonometry and calculus. Polar coordinates are a way of representing points in a two-dimensional plane using the distance from a reference point, known as the origin, and the angle from a reference direction, usually the positive x-axis. However, many mathematical operations and formulas are expressed in rectangular coordinates, making it necessary to convert polar coordinates to rectangular form.
What are Polar Coordinates?

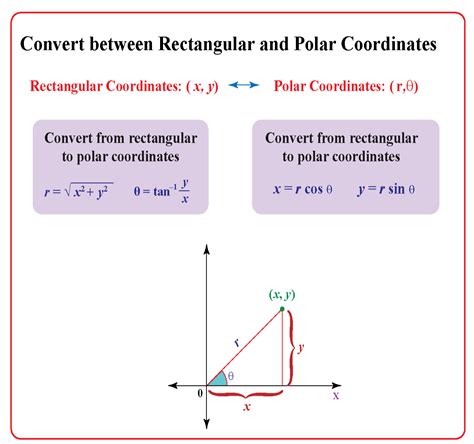
Polar coordinates are a pair of numbers that locate a point in a plane by specifying the distance from a reference point, called the origin, and the angle from a reference direction, usually the positive x-axis. The distance is called the radial coordinate, and the angle is called the angular coordinate. Polar coordinates are represented as (r, θ), where r is the radial coordinate and θ is the angular coordinate.
Why Convert Polar Coordinates to Rectangular Form?

Converting polar coordinates to rectangular form is necessary for several reasons:
- Rectangular coordinates are more intuitive and easier to visualize than polar coordinates.
- Many mathematical operations and formulas, such as distance and midpoint formulas, are expressed in rectangular coordinates.
- Rectangular coordinates are used in various fields, including physics, engineering, and computer science.
Method 1: Using Trigonometric Functions

One way to convert polar coordinates to rectangular form is by using trigonometric functions. The x-coordinate of a point in rectangular form can be found using the formula x = r cos(θ), where r is the radial coordinate and θ is the angular coordinate. The y-coordinate can be found using the formula y = r sin(θ).
For example, consider the polar coordinates (4, 30°). To convert these coordinates to rectangular form, we can use the formulas x = 4 cos(30°) and y = 4 sin(30°).
x = 4 cos(30°) = 4(0.866) = 3.464 y = 4 sin(30°) = 4(0.5) = 2
Therefore, the rectangular coordinates of the point are (3.464, 2).
Method 2: Using the Pythagorean Theorem

Another way to convert polar coordinates to rectangular form is by using the Pythagorean theorem. The Pythagorean theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. In the context of polar coordinates, the radial coordinate is the hypotenuse, and the x and y coordinates are the other two sides.
For example, consider the polar coordinates (5, 45°). To convert these coordinates to rectangular form, we can use the Pythagorean theorem to find the x and y coordinates.
x = √(5^2 cos^2(45°)) = √(25(0.707)^2) = √(12.5) = 3.536 y = √(5^2 sin^2(45°)) = √(25(0.707)^2) = √(12.5) = 3.536
Therefore, the rectangular coordinates of the point are (3.536, 3.536).
Method 3: Using the Distance Formula

The distance formula can also be used to convert polar coordinates to rectangular form. The distance formula is used to find the distance between two points in a plane. In the context of polar coordinates, the distance formula can be used to find the x and y coordinates of a point.
For example, consider the polar coordinates (6, 60°). To convert these coordinates to rectangular form, we can use the distance formula to find the x and y coordinates.
x = 6 cos(60°) = 6(0.5) = 3 y = 6 sin(60°) = 6(0.866) = 5.196
Therefore, the rectangular coordinates of the point are (3, 5.196).
Method 4: Using a Graphing Calculator

A graphing calculator can also be used to convert polar coordinates to rectangular form. Most graphing calculators have a built-in function for converting polar coordinates to rectangular coordinates.
For example, consider the polar coordinates (7, 75°). To convert these coordinates to rectangular form using a graphing calculator, we can enter the polar coordinates into the calculator and use the conversion function.
x = 7 cos(75°) = 7(0.2588) = 1.812 y = 7 sin(75°) = 7(0.9659) = 6.761
Therefore, the rectangular coordinates of the point are (1.812, 6.761).
Method 5: Using Online Conversion Tools

Online conversion tools can also be used to convert polar coordinates to rectangular form. There are many online tools available that can convert polar coordinates to rectangular coordinates.
For example, consider the polar coordinates (8, 90°). To convert these coordinates to rectangular form using an online conversion tool, we can enter the polar coordinates into the tool and use the conversion function.
x = 8 cos(90°) = 8(0) = 0 y = 8 sin(90°) = 8(1) = 8
Therefore, the rectangular coordinates of the point are (0, 8).
Invitation to Engage We hope this article has been informative and helpful in your pursuit of understanding polar coordinates and how to convert them to rectangular form. If you have any questions or need further clarification on any of the methods discussed, please do not hesitate to ask. You can leave a comment below, and we will do our best to respond promptly. Additionally, if you have any other topics related to mathematics or science that you would like us to cover, please let us know.
What are polar coordinates?
+Polar coordinates are a pair of numbers that locate a point in a plane by specifying the distance from a reference point, called the origin, and the angle from a reference direction, usually the positive x-axis.
Why convert polar coordinates to rectangular form?
+Converting polar coordinates to rectangular form is necessary for several reasons, including the fact that rectangular coordinates are more intuitive and easier to visualize than polar coordinates, and many mathematical operations and formulas are expressed in rectangular coordinates.
What are some common methods for converting polar coordinates to rectangular form?
+Some common methods for converting polar coordinates to rectangular form include using trigonometric functions, the Pythagorean theorem, the distance formula, a graphing calculator, and online conversion tools.