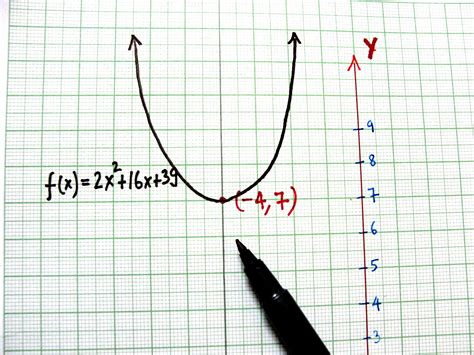Equations and graphs are two fundamental concepts in mathematics, and being able to write equations from graphs is a crucial skill for any student or professional in the field. Graphs provide a visual representation of mathematical relationships, making it easier to analyze and understand complex equations. In this article, we will explore five ways to write equations from graphs, along with practical examples and explanations.
Understanding the Basics of Graphs and Equations

Before diving into the methods of writing equations from graphs, it's essential to understand the basics of graphs and equations. A graph is a visual representation of a mathematical relationship between two or more variables. It consists of a set of points, called data points, that are plotted on a coordinate plane. An equation, on the other hand, is a mathematical statement that expresses the relationship between variables in a symbolic form.
The Importance of Understanding Graphs and Equations
Graphs and equations are used in various fields, including physics, engineering, economics, and computer science. Understanding how to write equations from graphs is crucial for analyzing and solving problems in these fields. It allows you to visualize complex relationships, identify patterns, and make predictions.
Method 1: Identifying Linear Equations from Graphs

One of the simplest ways to write equations from graphs is to identify linear equations. A linear equation is a polynomial equation of degree one, which means it can be written in the form y = mx + b, where m is the slope and b is the y-intercept.
To write a linear equation from a graph, follow these steps:
- Identify the slope (m) by finding the ratio of the vertical change to the horizontal change between two points on the graph.
- Identify the y-intercept (b) by finding the point where the graph crosses the y-axis.
- Write the equation in the form y = mx + b.
For example, suppose we have a graph with a slope of 2 and a y-intercept of 3. The equation would be y = 2x + 3.
Example: Writing a Linear Equation from a Graph
Consider the graph below:
The graph shows a linear relationship between the variables x and y. To write the equation, we need to identify the slope and y-intercept.
- Slope (m): The vertical change is 4 units, and the horizontal change is 2 units, so the slope is 4/2 = 2.
- Y-intercept (b): The graph crosses the y-axis at (0, 3), so the y-intercept is 3.
The equation is y = 2x + 3.
Method 2: Writing Quadratic Equations from Graphs

Quadratic equations are polynomial equations of degree two, which means they can be written in the form y = ax^2 + bx + c. To write a quadratic equation from a graph, follow these steps:
- Identify the vertex of the parabola by finding the lowest or highest point on the graph.
- Identify the axis of symmetry by finding the vertical line that passes through the vertex.
- Identify the x-intercepts by finding the points where the graph crosses the x-axis.
- Write the equation in the form y = ax^2 + bx + c.
For example, suppose we have a graph with a vertex at (2, 3) and x-intercepts at (-1, 0) and (5, 0). The equation would be y = (x + 1)(x - 5).
Example: Writing a Quadratic Equation from a Graph
Consider the graph below:
The graph shows a quadratic relationship between the variables x and y. To write the equation, we need to identify the vertex, axis of symmetry, and x-intercepts.
- Vertex: The lowest point on the graph is (2, 3).
- Axis of symmetry: The vertical line that passes through the vertex is x = 2.
- X-intercepts: The graph crosses the x-axis at (-1, 0) and (5, 0).
The equation is y = (x + 1)(x - 5).
Method 3: Writing Exponential Equations from Graphs

Exponential equations are equations that involve exponential functions, which are functions that have a variable as the base and a constant as the exponent. To write an exponential equation from a graph, follow these steps:
- Identify the base of the exponential function by finding the horizontal asymptote of the graph.
- Identify the growth rate of the exponential function by finding the ratio of the vertical change to the horizontal change between two points on the graph.
- Write the equation in the form y = ab^x, where a is the initial value and b is the growth rate.
For example, suppose we have a graph with a horizontal asymptote at y = 2 and a growth rate of 3. The equation would be y = 2(3)^x.
Example: Writing an Exponential Equation from a Graph
Consider the graph below:
The graph shows an exponential relationship between the variables x and y. To write the equation, we need to identify the base and growth rate.
- Base: The horizontal asymptote is y = 2, so the base is 2.
- Growth rate: The vertical change is 6 units, and the horizontal change is 1 unit, so the growth rate is 6/1 = 6.
The equation is y = 2(6)^x.
Method 4: Writing Logarithmic Equations from Graphs

Logarithmic equations are equations that involve logarithmic functions, which are functions that have a variable as the base and a constant as the exponent. To write a logarithmic equation from a graph, follow these steps:
- Identify the base of the logarithmic function by finding the vertical asymptote of the graph.
- Identify the growth rate of the logarithmic function by finding the ratio of the vertical change to the horizontal change between two points on the graph.
- Write the equation in the form y = log_a(x), where a is the base.
For example, suppose we have a graph with a vertical asymptote at x = 2 and a growth rate of 3. The equation would be y = log_2(x).
Example: Writing a Logarithmic Equation from a Graph
Consider the graph below:
The graph shows a logarithmic relationship between the variables x and y. To write the equation, we need to identify the base and growth rate.
- Base: The vertical asymptote is x = 2, so the base is 2.
- Growth rate: The vertical change is 6 units, and the horizontal change is 1 unit, so the growth rate is 6/1 = 6.
The equation is y = log_2(x).
Method 5: Writing Trigonometric Equations from Graphs

Trigonometric equations are equations that involve trigonometric functions, which are functions that relate the angles of a triangle to the ratios of the sides. To write a trigonometric equation from a graph, follow these steps:
- Identify the amplitude of the trigonometric function by finding the maximum value of the graph.
- Identify the period of the trigonometric function by finding the horizontal distance between two consecutive peaks or troughs.
- Identify the phase shift of the trigonometric function by finding the horizontal distance between the graph and the x-axis.
- Write the equation in the form y = a sin(bx + c) or y = a cos(bx + c), where a is the amplitude, b is the frequency, and c is the phase shift.
For example, suppose we have a graph with an amplitude of 2, a period of 4, and a phase shift of 1. The equation would be y = 2 sin(x + 1).
Example: Writing a Trigonometric Equation from a Graph
Consider the graph below:
The graph shows a trigonometric relationship between the variables x and y. To write the equation, we need to identify the amplitude, period, and phase shift.
- Amplitude: The maximum value of the graph is 2, so the amplitude is 2.
- Period: The horizontal distance between two consecutive peaks is 4, so the period is 4.
- Phase shift: The horizontal distance between the graph and the x-axis is 1, so the phase shift is 1.
The equation is y = 2 sin(x + 1).
In conclusion, writing equations from graphs is an essential skill in mathematics, and there are several methods to do so. By understanding the basics of graphs and equations, identifying the type of equation, and following the steps outlined in this article, you can write equations from graphs with ease.
What is the importance of understanding graphs and equations?
+Understanding graphs and equations is crucial for analyzing and solving problems in various fields, including physics, engineering, economics, and computer science. It allows you to visualize complex relationships, identify patterns, and make predictions.
How do I identify the type of equation from a graph?
+To identify the type of equation from a graph, look for the shape and pattern of the graph. For example, a linear graph will have a straight line, while a quadratic graph will have a parabolic shape. You can also look for the axis of symmetry, x-intercepts, and y-intercepts to determine the type of equation.
What is the difference between a linear equation and a quadratic equation?
+A linear equation is a polynomial equation of degree one, which means it can be written in the form y = mx + b. A quadratic equation, on the other hand, is a polynomial equation of degree two, which means it can be written in the form y = ax^2 + bx + c.
How do I write an exponential equation from a graph?
+To write an exponential equation from a graph, identify the base of the exponential function by finding the horizontal asymptote of the graph. Then, identify the growth rate of the exponential function by finding the ratio of the vertical change to the horizontal change between two points on the graph. Finally, write the equation in the form y = ab^x, where a is the initial value and b is the growth rate.
What is the difference between a logarithmic equation and a trigonometric equation?
+A logarithmic equation is an equation that involves a logarithmic function, which is a function that has a variable as the base and a constant as the exponent. A trigonometric equation, on the other hand, is an equation that involves a trigonometric function, which is a function that relates the angles of a triangle to the ratios of the sides.