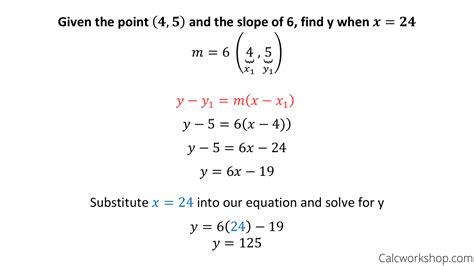5 Easy Steps To Master Point Slope Form Answer Key

Quick Links :

In mathematics, particularly in algebra, understanding the point-slope form is a crucial skill for graphing linear equations. This concept is fundamental in mathematics and is used extensively in various fields such as physics, engineering, and economics. Mastering the point-slope form not only enhances problem-solving skills but also provides a deeper understanding of linear equations. Here, we'll break down the point-slope form into 5 easy steps to make it accessible to everyone.

Understanding the Point-Slope Form

The point-slope form of a linear equation is y - y1 = m(x - x1), where m is the slope of the line, and (x1, y1) is a point on the line. This form is particularly useful for finding the equation of a line when we know its slope and a point it passes through.

Benefits of Mastering Point-Slope Form

Mastering the point-slope form has several benefits:

• It allows you to find the equation of a line when given the slope and a point on the line.
• It's useful for graphing linear equations, especially when you're given two points and need to find the slope.
• It helps in solving problems involving linear equations, making it a valuable tool in algebra and other branches of mathematics.

Step 1: Identify the Slope and Point

The first step is to identify the slope (m) and the point (x1, y1) given in the problem. The slope can be calculated using the formula m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line. However, in many cases, the slope and a point on the line are provided directly.

Example

For instance, if we are given that the slope (m) is 2 and the point (x1, y1) is (3, 4), we can directly use these values in the point-slope form.

Step 2: Plug the Values into the Point-Slope Form

Once you have identified the slope and the point, plug these values into the point-slope form equation y - y1 = m(x - x1). Using the example from Step 1, the equation becomes y - 4 = 2(x - 3).

Example Calculation

Plugging in the slope and point given in the example:

• Slope (m) = 2
• Point (x1, y1) = (3, 4)
• Equation: y - 4 = 2(x - 3)

Step 3: Simplify the Equation

After plugging in the values, simplify the equation. Distribute the slope (m) across the terms in the parentheses and combine like terms.

Example Simplification

Continuing with our example:

• y - 4 = 2(x - 3)
• Distributing: y - 4 = 2x - 6
• Adding 4 to both sides to isolate y: y = 2x - 2

Step 4: Graph the Line (Optional)

If required, use the simplified equation to graph the line. Knowing the slope and a point on the line makes graphing straightforward. Plot the point and use the slope to find another point, then draw the line through these points.

Graphing Tips

• Always plot the given point first.
• Use the slope to determine the direction and steepness of the line.
• Plot another point based on the slope and draw the line.

Step 5: Practice and Apply

The final step is to practice using the point-slope form with different slopes and points. The more you practice, the more comfortable you'll become with this form. Try applying it to various problems, including those involving real-world applications.

Practice Tips

• Start with simple slopes (e.g., 1, -1, 2, -2) and gradually move to more complex ones.
• Use online resources or math worksheets for practice problems.
• Mix up the points and slopes to cover a wide range of scenarios.

By following these 5 easy steps, you'll master the point-slope form and improve your skills in graphing and solving linear equations. Remember, practice is key to becoming proficient, so don't hesitate to apply these steps to various problems.

If you've found this guide helpful, consider sharing it with others who might benefit from mastering the point-slope form. Have any questions or need further clarification on any of the steps? Please don't hesitate to ask in the comments below!