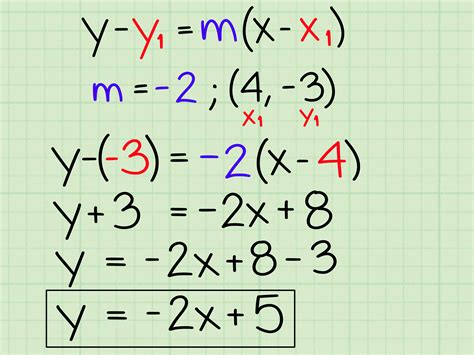Mastering The Parallel Slope Intercept Form Easily

Quick Links :

The slope-intercept form of a linear equation is one of the most popular and widely used forms in mathematics, particularly in algebra and geometry. However, there is another crucial aspect of linear equations that is often overlooked - the parallel slope-intercept form. In this article, we will delve into the world of parallel slope-intercept form, exploring its definition, importance, and practical applications. We will also provide step-by-step instructions on how to master this essential concept with ease.

Understanding the Slope-Intercept Form

Before we dive into the parallel slope-intercept form, let's quickly review the slope-intercept form. The slope-intercept form of a linear equation is represented as y = mx + b, where m is the slope of the line and b is the y-intercept. This form is widely used to represent linear equations in various mathematical and real-world applications.

The Importance of Slope-Intercept Form

The slope-intercept form is essential in mathematics and real-world applications because it provides a clear and concise way to represent linear equations. It allows us to easily identify the slope and y-intercept of a line, which is crucial in graphing, solving systems of equations, and modeling real-world phenomena.

What is Parallel Slope-Intercept Form?

Now that we have reviewed the slope-intercept form, let's explore the parallel slope-intercept form. The parallel slope-intercept form is a way to represent two or more linear equations that have the same slope but different y-intercepts. This form is represented as y = mx + b1 and y = mx + b2, where m is the slope and b1 and b2 are the y-intercepts.

Why is Parallel Slope-Intercept Form Important?

The parallel slope-intercept form is crucial in mathematics and real-world applications because it allows us to compare and contrast two or more linear equations that have the same slope but different y-intercepts. This form is essential in graphing, solving systems of equations, and modeling real-world phenomena, such as comparing the growth rates of different investments or the costs of different services.

How to Master Parallel Slope-Intercept Form

Mastering the parallel slope-intercept form requires practice and patience. Here are some step-by-step instructions to help you master this essential concept:

1. Understand the Slope-Intercept Form: Before you can master the parallel slope-intercept form, you need to understand the slope-intercept form. Make sure you can identify the slope and y-intercept of a linear equation in slope-intercept form.
2. Practice Writing Parallel Equations: Practice writing two or more linear equations that have the same slope but different y-intercepts. For example, y = 2x + 3 and y = 2x + 5.
3. Graph Parallel Equations: Graph two or more parallel equations on the same coordinate plane. This will help you visualize the relationship between the equations and understand how they intersect.
4. Solve Systems of Parallel Equations: Practice solving systems of parallel equations using substitution or elimination methods. This will help you understand how to compare and contrast two or more linear equations.
5. Apply Parallel Slope-Intercept Form to Real-World Problems: Practice applying the parallel slope-intercept form to real-world problems, such as comparing the growth rates of different investments or the costs of different services.

Real-World Applications of Parallel Slope-Intercept Form

The parallel slope-intercept form has numerous real-world applications in fields such as business, economics, science, and engineering. Here are a few examples:

1. Comparing Investment Growth Rates: The parallel slope-intercept form can be used to compare the growth rates of different investments, such as stocks or bonds.
2. Modeling Cost-Benefit Analysis: The parallel slope-intercept form can be used to model the cost-benefit analysis of different services or products.
3. Predicting Population Growth: The parallel slope-intercept form can be used to predict population growth rates and compare the growth rates of different cities or countries.

Conclusion

In conclusion, the parallel slope-intercept form is an essential concept in mathematics and real-world applications. By mastering this concept, you can compare and contrast two or more linear equations that have the same slope but different y-intercepts. With practice and patience, you can apply the parallel slope-intercept form to real-world problems and become a proficient mathematician.